题目内容
若函数y=f（x）（x∈R）满足f（x+2）=f（x），且x∈[-1，1]时，f（x）=2x+x
，则f（2014）等于（ ）
| 1 |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
考点：函数的值,函数的周期性
专题：函数的性质及应用
分析：根据函数的周期性，将函数值进行转化即可．
解答：
解：因为f（x+2）=f（x），
所以f（x）的周期为2，
则f（2014）=f（0）=20+0
=1．
故选：C
所以f（x）的周期为2，
则f（2014）=f（0）=20+0
| 1 |
| 3 |
故选：C
点评：本题主要考查函数值的计算，根据函数的周期性，进行转化是解决本题的关键．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
下列函数f（x）与g（x）相等的一组是（ ）
A、f（x）=x-1，g（x）=
| ||
B、f（x）=x2，g（x）=（
| ||
| C、f（x）=log2x2，g（x）=2log2x | ||
D、f（x）=tanx，g（x）=
|
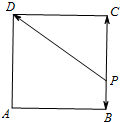如图，正方形ABCD的边长为2，点P是线段BC上的动点，则（