题目内容
已知sinα=
,则sin4α-cos4α的值为 .
| ||
| 5 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由sinα的值,求出cos2α的值,原式利用平方差公式化简,再利用同角三角函数间的基本关系变形,将各自的值代入计算即可求出值.
解答:
解:∵sinα=
,
∴cos2α=1-sin2α=
,
则原式=(sin2α-cos2α)(sin2α+cos2α)=sin2α-cos2α=
-
=-
.
故答案为:-
| ||
| 5 |
∴cos2α=1-sin2α=
| 4 |
| 5 |
则原式=(sin2α-cos2α)(sin2α+cos2α)=sin2α-cos2α=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
故答案为:-
| 3 |
| 5 |
点评:此题考查了同角三角函数关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
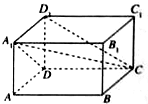 在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.
在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.