题目内容
2.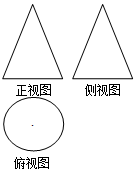 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $2\sqrt{2}π$ | C. | $8\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}}}{3}π$ |
分析 由三视图可知:该几何体为一个圆锥.利用体积计算公式即可得出.
解答 解:由三视图可知:该几何体为一个圆锥.底面半径为1,母线长为:3,高为$\sqrt{9-1}$=2$\sqrt{2}$;
其体积=$\frac{1}{3}$π×12×2$\sqrt{2}$=$\frac{2\sqrt{2}}{3}$π.
故选:A.
点评 本题考查了三视图的有关知识、圆锥的体积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
5.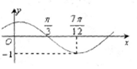 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
7.已知命题p:?x∈R,sinx>1,则( )
| A. | ?p:?x∈R,sinx≤1 | B. | ?p:?x∈R,sinx≤1 | C. | ?p:?x∈R,sinx≤1 | D. | ?p:?x∈R,sinx>1 |
14.函数f(x)=ax3+bx2+cx-34(a,b,c∈R)的导函数为f′(x),若不等式f′(x)≤0的解集为{x|-2≤x≤3},且f(x)的极小值等于-196,则a的值是( )
| A. | -$\frac{81}{22}$ | B. | $\frac{1}{3}$ | C. | 5 | D. | .4 |
11.cos(π-α)=( )
| A. | cosα | B. | -cosα | C. | sinα | D. | -sinα |
12.若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)≤0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
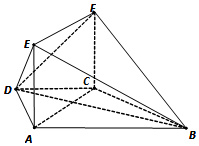 在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.
在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.