题目内容
14．函数f（x）=ax3+bx2+cx-34（a，b，c∈R）的导函数为f′（x），若不等式f′（x）≤0的解集为{x|-2≤x≤3}，且f（x）的极小值等于-196，则a的值是（ ）| A． | -$\frac{81}{22}$ | B． | $\frac{1}{3}$ | C． | 5 | D． | ．4 |
分析 求导数，利用韦达定理，结合f（x）的极小值等于-196，即可求出a的值．
解答 解：依题意得f′（x）=3ax2+2bx+c≤0的解集是[-2，3]，
于是有3a＞0，-2+3=-$\frac{2b}{3a}$，-2×3=$\frac{c}{3a}$，
解得b=-$\frac{3a}{2}$，c=-18a，
∵函数f（x）在x=3处取得极小值，
∴有f（3）=27a+9b+3c-34=-196，
∴a=4，
故选：D．
点评 本题考查利用导数研究函数的极值，考查韦达定理的运用，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
5．运行以下程序框图，若输入的$x∈[{-\frac{π}{2}，\frac{π}{2}}]$，则输出的y的范围是（ ）
| A． | [-1，1] | B． | [-1，0] | C． | [0，1] | D． | （0，1] |
2．
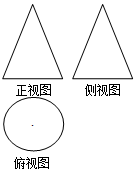如图是一个几何体的三视图，其中正视图和侧视图都是腰长为3，底边长为2的等腰三角形，则该几何体的体积是（ ）
如图是一个几何体的三视图，其中正视图和侧视图都是腰长为3，底边长为2的等腰三角形，则该几何体的体积是（ ）| A． | $\frac{{2\sqrt{2}}}{3}π$ | B． | $2\sqrt{2}π$ | C． | $8\sqrt{2}π$ | D． | $\frac{{8\sqrt{2}}}{3}π$ |
9．
如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为$4\sqrt{3}$，则这个圆锥的体积为（ ）
如图，一竖立在地面上的圆锥形物体的母线长为4，一只小虫从圆锥的底面圆上的点P出发，绕圆锥爬行一周后回到点P处，若该小虫爬行的最短路程为$4\sqrt{3}$，则这个圆锥的体积为（ ）| A． | $\frac{{\sqrt{15}}}{3}$ | B． | $\frac{{32\sqrt{35}π}}{27}$ | C． | $\frac{{128\sqrt{2}π}}{81}$ | D． | $\frac{{8\sqrt{3}}}{3}$ |
6．设a=1og1.20.8，b=1og0.70.8，c=1.20.8，则a，b，c的大小关系是（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | a＜c＜b | D． | c＜a＜b |