题目内容
17.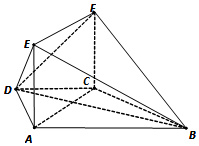 在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.
在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)求二面角B-EF-D的余弦值.
分析 (Ⅰ)推导出AC⊥BC,由此能证明BC⊥平面ACFE.
(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,推导出∠DGH是二面角B-EF-D的平面角,由此能求出二面角B-EF-D的平面角余弦值.
解答 证明:(Ⅰ)在梯形ABCD中,
∵AB∥CD,AD=DC=a,∠ABC=60°,
∴四边形ABCD是等腰梯形,且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=∠DCB-∠DCA=90°,∴AC⊥BC,
又∵平面ACEF⊥平面ABCD,交线为AC,∴BC⊥平面ACFE.
解:(Ⅱ)取EF中点G,EB中点H,连结DG、GH、DH,
由题意得DE=DF,∴DG⊥EF,
∵BC⊥平面ACFE,∴BC⊥EF,
又∵EF⊥FC,∴EF⊥FB,
又∵GH∥FB,∴EF⊥GH,
∴∠DGH是二面角B-EF-D的平面角.
在△BDE中,DE=2$\sqrt{2}$,DB=2$\sqrt{3}$,BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=2$\sqrt{5}$,
∴BE2=DE2+DB2,∴∠EDB=90°,∴DH=$\sqrt{5}$,
又DG=$\sqrt{5}$,GH=$\sqrt{2}$,∴在△DGH中,由余弦定理得cos∠DGH=$\frac{D{G}^{2}+G{H}^{2}-D{H}^{2}}{2DG•GH}$=$\frac{\sqrt{10}}{10}$,
即二面角B-EF-D的平面角余弦值为$\frac{\sqrt{10}}{10}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,考查空间想象能力、推理论证能力、数形结合思想、转化思想以及计算能力,是中档题.

练习册系列答案
相关题目
8.已知直线l经过点(0,-2),其倾斜角的大小是60°,则直线l与两坐标轴围成三角形的面积S等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{3\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
5.运行以下程序框图,若输入的$x∈[{-\frac{π}{2},\frac{π}{2}}]$,则输出的y的范围是( )


| A. | [-1,1] | B. | [-1,0] | C. | [0,1] | D. | (0,1] |
2.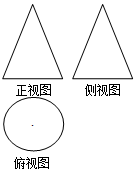 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $2\sqrt{2}π$ | C. | $8\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}}}{3}π$ |
9. 如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为$4\sqrt{3}$,则这个圆锥的体积为( )
如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为$4\sqrt{3}$,则这个圆锥的体积为( )
 如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为$4\sqrt{3}$,则这个圆锥的体积为( )
如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为$4\sqrt{3}$,则这个圆锥的体积为( )| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{32\sqrt{35}π}}{27}$ | C. | $\frac{{128\sqrt{2}π}}{81}$ | D. | $\frac{{8\sqrt{3}}}{3}$ |
6.设a=1og1.20.8,b=1og0.70.8,c=1.20.8,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<a<b |