题目内容
7．已知命题p：?x∈R，sinx＞1，则（ ）| A． | ?p：?x∈R，sinx≤1 | B． | ?p：?x∈R，sinx≤1 | C． | ?p：?x∈R，sinx≤1 | D． | ?p：?x∈R，sinx＞1 |
分析 原命题是特称命题，其否定为全称命题，将“存在”改为“任意的”，“＞“改为“≤”即可得答案．
解答 解：∵命题p：“?x∈R，sinx＞1，”是特称命题，
∴?p：?x∈R，sinx≤1
故选：C
点评 本题主要考查全称命题与特称命题的相互转化问题．这里注意全称命题的否定为特称命题，反过来特称命题的否定是全称命题．
练习册系列答案
相关题目
18．将两颗骰子各掷一次，设事件A为“两个点数相同”则概率P（A）等于（ ）
| A． | $\frac{10}{11}$ | B． | $\frac{5}{11}$ | C． | $\frac{1}{6}$ | D． | $\frac{5}{36}$ |
15．.假设某设备的使用年限x（年）和所支出的维修费用y（万元）有如下的统计资料：
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
试求：（1）y与x之间的回归方程；
（2）当使用年限为10年时，估计维修费用是多少？
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求：（1）y与x之间的回归方程；
（2）当使用年限为10年时，估计维修费用是多少？
2．
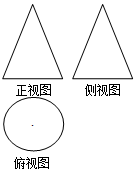如图是一个几何体的三视图，其中正视图和侧视图都是腰长为3，底边长为2的等腰三角形，则该几何体的体积是（ ）
如图是一个几何体的三视图，其中正视图和侧视图都是腰长为3，底边长为2的等腰三角形，则该几何体的体积是（ ）| A． | $\frac{{2\sqrt{2}}}{3}π$ | B． | $2\sqrt{2}π$ | C． | $8\sqrt{2}π$ | D． | $\frac{{8\sqrt{2}}}{3}π$ |
12．下列说法中正确的是（ ）
| A． | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$，则$\vec b=\overrightarrow c$ | |
| B． | 若$\overrightarrow a•\overrightarrow b=0$，则$\vec a=\vec 0$或$\vec b=\vec 0$ | |
| C． | 若不平行的两个非零向量$\overrightarrow a，\overrightarrow b$满足$|\overrightarrow a|=|\overrightarrow b|$，则$（\overrightarrow a+\overrightarrow b）•（\overrightarrow a-\overrightarrow b）=0$ | |
| D． | 若$\overrightarrow a$与$\overrightarrow b$平行，则$\overrightarrow a•\overrightarrow b=|\overrightarrow a|•|\overrightarrow b|$ |