题目内容
5.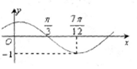 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
分析 利用函数的图象求出函数的周期,然后求出ω,通过函数图象经过的特殊点求出φ,进而利用函数y=Asin(ωx+φ)的图象变换规律即可得解.
解答 解:由函数的图象可知函数的周期为:T=4×($\frac{7π}{12}$-$\frac{π}{3}$)=π,
所以:ω=$\frac{2π}{π}$=2,
因为:图象经过($\frac{π}{3}$,0),
所以:0=sin(2×$\frac{π}{3}$+φ),可得:2×$\frac{π}{3}$+φ=kπ,k∈Z,
因为:|φ|<$\frac{π}{2}$,
所以:φ=$\frac{π}{3}$,可得:f(x)=sin(2x+$\frac{π}{3}$)=sin[2(x+$\frac{π}{6}$)],
所以:将f(x)的图象向右平移$\frac{π}{6}$个单位长度即可得到g(x)=sin2x的图象,
故选:C.
点评 本题考查三角函数的解析式的求法,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,考查计算能力和数形结合思想,属于基础题.

练习册系列答案
相关题目
13.定义在R上的函数f(x)满足:f'(x)>2-f(x),f(0)=6,f'(x)是f(x)的导函数,则不等式exf(x)>2ex+4(其中e为自然对数的底数)的解集为( )
| A. | (0,+∞) | B. | (-∞,0)∪(3,+∞) | C. | (-∞,0)∪(1,+∞) | D. | (3,+∞) |
1.若函数f(x)=2x3-3mx2+6x在区间(1,+∞)上为增函数,则实数m的取值范围是( )
| A. | (-∞,1] | B. | (-∞,1) | C. | (-∞,2] | D. | (-∞,2) |
2.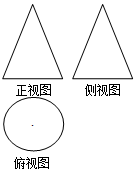 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
 如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是腰长为3,底边长为2的等腰三角形,则该几何体的体积是( )| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $2\sqrt{2}π$ | C. | $8\sqrt{2}π$ | D. | $\frac{{8\sqrt{2}}}{3}π$ |
 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点.