题目内容
已知直线x=a（a＜0）与函数y=（
） x，y=(
)x，y=2x，y=10x的图象依次交与A，B，C，D四点，则这四个点从上到下的排列次序是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、A、B、C、D |
| B、B、C、A、D |
| C、B、A、C、D |
| D、C、A、B、D |
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：取特殊值令x=-1，分别求出与函数的交点的纵坐标，由此即可以判定这四点从上到下的排列次序．
解答：
解，不妨令x=-1＜0，
∴函数值yA=(
)-1=3，yB=(
)-1=2，yC=2-1=
，yD=10-1=
；
∵yA＞yB＞yC＞yD，
∴点A，B，C，D从上到下的排列次序是A，B，C，D；
故选：A．
∴函数值yA=(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 10 |
∵yA＞yB＞yC＞yD，
∴点A，B，C，D从上到下的排列次序是A，B，C，D；
故选：A．
点评：本题考查了指数函数的图象与性质的应用问题，是基础题．
练习册系列答案
相关题目
将某选手的7个得分去掉1个最高分，去掉1个最低分，剩余5个得分的平均分为91，现场做的7个得分的茎叶图（如图）后来有一个数据模糊，无法辨认，在图中用x表示，则x的值为（ ）公务员考试分笔试和面试，笔试的通过率为20%，最后的录取率为4%，已知某人已经通过笔试，则他最后被录取的概率为（ ）
| A、20% | B、24% |
| C、16% | D、4% |
函数f（x）=
，满足对任意定义域中的x1，x2（x1≠x2），[f（x1）-f（x2）]（x1-x2）＜0总成立，则实数a的取值范围是（ ）
|
| A、（-∞，0） |
| B、[-1，0） |
| C、（-1，0） |
| D、（-1，+∞）， |
定义域为R的函数f(x)=
，若关于x的方程f2（x）-af（x）+b=0有3个不同实数解x1，x2，x3，且x1＜x2＜x3，则下列说法错误的是（ ）
|
|
| A、5+b-2a=1 |
| B、b＜0 |
| C、x1-x2+x3=3 |
| D、x12+x22+x32=9 |
对于R上可导的任意函数f（x），若满足
≤0，则必有（ ）
| 2-x |
| f′(x) |
| A、f（1）+f（3）＜2f（2） |
| B、f（1）+f（3）≤2f（2） |
| C、f（1）+f（3）＞2f（2） |
| D、f（1）+f（3）≥2f（2） |
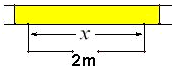围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．