题目内容
随机变量ξ服从二项分布ξ～B（16，P），且Dξ=3，则Eξ等于（ ）
| A、4 | B、12 | C、4或12 | D、3 |
考点：二项分布与n次独立重复试验的模型
专题：计算题,概率与统计
分析：随机变量ξ服从二项分布，故可直接利用方差公式进行计算，求出P，即可求出Eξ．
解答：
解：∵随机变量ξ服从二项分布ξ～B（16，P），且Dξ=3，
∴Dξ=16P（1-P）=3，
∴P=
或P=
∴Eξ=nP=4或12．
故选C．
∴Dξ=16P（1-P）=3，
∴P=
| 1 |
| 4 |
| 3 |
| 4 |
∴Eξ=nP=4或12．
故选C．
点评：本题主要考查二项分布的方差和期望的简单应用，考查学生的计算能力，正确运用公式是关键．
练习册系列答案
相关题目
将某选手的7个得分去掉1个最高分，去掉1个最低分，剩余5个得分的平均分为91，现场做的7个得分的茎叶图（如图）后来有一个数据模糊，无法辨认，在图中用x表示，则x的值为（ ）定义域为R的函数f(x)=
，若关于x的方程f2（x）-af（x）+b=0有3个不同实数解x1，x2，x3，且x1＜x2＜x3，则下列说法错误的是（ ）
|
|
| A、5+b-2a=1 |
| B、b＜0 |
| C、x1-x2+x3=3 |
| D、x12+x22+x32=9 |
对于R上可导的任意函数f（x），若满足
≤0，则必有（ ）
| 2-x |
| f′(x) |
| A、f（1）+f（3）＜2f（2） |
| B、f（1）+f（3）≤2f（2） |
| C、f（1）+f（3）＞2f（2） |
| D、f（1）+f（3）≥2f（2） |
从含有两件正品和一件次品的三件产品中，每次随机取一件，连结取两次，每次取后都放回，则取出的两件产品中恰有一件次的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
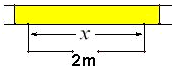围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．