题目内容
已知数列{an}的前n项和为Sn,且满足Sn=-
an-
(n∈N*)
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=
,证明:对于一切正整数n,不等式b1×b2×b3×…×bn<2×n!恒成立.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=
| n |
| an+1 |
考点:数学归纳法,数列的求和
专题:证明题,点列、递归数列与数学归纳法
分析:(1)由Sn=-
an-
①,知Sn-1=-
an-1-
(n≥2)②,两式相减后整理后,易证数列{an}为以a1=-
为首项,
为公比的等比数列,从而可求数列{an}的通项公式;
(2)由bn=
=
(n∈N*),可知b1×b2×b3×…×bn=
,要证b1×b2×b3×…×bn<2×n!,只要证(1-
)(1-
)…(1-
)>
,利用数学归纳法证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)由bn=
| n |
| an+1 |
| n | ||
1-
|
| n! | ||||||||
(1-
|
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 1 |
| 2 |
解答:
解:(1)由Sn=-
an-
①,
得Sn-1=-
an-1-
(n≥2)②,
由①-②,得an=-
an+
an-1,即3an=an-1(n≥2).
由S1=-
a1-
,得a1=-
,
∴数列{an}为以a1=-
为首项,
为公比的等比数列,
即an=-
•(
)n-1=-(
)n(n∈N*).
(2)证明:由
bn=
=
(n∈N*),
得:b1×b2×b3×…×bn=
=
.
因此,要证b1×b2×b3×…×bn<2×n!,
只要证(1-
)(1-
)…(1-
)>
.
下面用数学归纳法先证明(1-
)(1-
)…(1-
)≥1-(
+
+…+
)(n∈N*).
①当n=1,不等式左边=
,右边=
,
∴不等式成立;
②设n=k(k≥1,k∈N*)时,不等式成立,
即(1-
)(1-
)…(1-
)≥1-(
+
+…+
)(k∈N*),
则当n=k+1时,
左边=(1-
)(1-
)…(1-
)(1-
)≥[1-(
+
+…+
)](1-
),
而[1-(
+
+…+
)]•(1-
)=1-
-(
+
+…+
)+
(
+
+…+
)≥1-(
+
+…+
+
),
即n=k+1时,不等式也成立.
综合①②,(1-
)(1-
)…(1-
)≥1-(
+
+…+
)(n∈N*).成立.
又1-(
+
+…+
)=1-
=
+
>
,
∴(1-
)(1-
)…(1-
)>
.成立.
从而b1×b2×b3×…×bn<2×n!成立.
| 1 |
| 2 |
| 1 |
| 2 |
得Sn-1=-
| 1 |
| 2 |
| 1 |
| 2 |
由①-②,得an=-
| 1 |
| 2 |
| 1 |
| 2 |
由S1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴数列{an}为以a1=-
| 1 |
| 3 |
| 1 |
| 3 |
即an=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)证明:由
bn=
| n |
| an+1 |
| n | ||
1-
|
得:b1×b2×b3×…×bn=
| 1×2×3×…×n | ||||||||
(1-
|
| n! | ||||||||
(1-
|
因此,要证b1×b2×b3×…×bn<2×n!,
只要证(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 1 |
| 2 |
下面用数学归纳法先证明(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
①当n=1,不等式左边=
| 2 |
| 3 |
| 2 |
| 3 |
∴不等式成立;
②设n=k(k≥1,k∈N*)时,不等式成立,
即(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
则当n=k+1时,
左边=(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
而[1-(
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3k+1 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
即n=k+1时,不等式也成立.
综合①②,(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
又1-(
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2×3n |
| 1 |
| 2 |
∴(1-
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 1 |
| 2 |
从而b1×b2×b3×…×bn<2×n!成立.
点评:本题考查递推数列,考查数列等比关系的确定,着重考查数学归纳法的应用,考查分析法,推理与证明的能力,属于难题.

练习册系列答案
相关题目
公务员考试分笔试和面试,笔试的通过率为20%,最后的录取率为4%,已知某人已经通过笔试,则他最后被录取的概率为( )
| A、20% | B、24% |
| C、16% | D、4% |
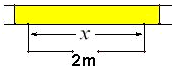 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).