题目内容
下列函数中，与函数f(x)=
的奇偶性、单调性均相同的是（ ）
| ex-e-x |
| 3 |
A、y=ln(x+
| ||
| B、y=x2 | ||
| C、y=tanx | ||
| D、y=ex |
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：先判断函数f（x）的奇偶性和单调性，然后再分别判断即可得到结论．
解答：
解：∵f（-x）=
=-
=-f(x)，
∴函数f（x）是奇函数且为增函数．
A.f(-x)=ln?(-x+
)=ln?
=ln?
=-ln?(x+
)=-f(x)，为奇函数，根据复合函数的单调性可知函数为增函数．
B．为偶函数，在定义域上不单调．
C．为奇函数，在定义域上不单调．
D．在定义域上单调递增，为非奇非偶函数．
故选：A．
| e-x-ex |
| 3 |
| ex-e-x |
| 3 |
∴函数f（x）是奇函数且为增函数．
A.f(-x)=ln?(-x+
| x2+1 |
(-x+
| ||||
(x+
|
| 1 | ||
(x+
|
| x2+1 |
B．为偶函数，在定义域上不单调．
C．为奇函数，在定义域上不单调．
D．在定义域上单调递增，为非奇非偶函数．
故选：A．
点评：本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
对于R上可导的任意函数f（x），若满足
≤0，则必有（ ）
| 2-x |
| f′(x) |
| A、f（1）+f（3）＜2f（2） |
| B、f（1）+f（3）≤2f（2） |
| C、f（1）+f（3）＞2f（2） |
| D、f（1）+f（3）≥2f（2） |
从含有两件正品和一件次品的三件产品中，每次随机取一件，连结取两次，每次取后都放回，则取出的两件产品中恰有一件次的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
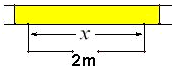围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．