题目内容
已知双曲线
-y2=1(a>1)的一个焦点为F,点P在双曲线上,且|
|=|
|(O为坐标原点),则△OPF的面积S= .
| x2 |
| a2 |
| OP |
| OF |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线的参数方程设出P的坐标,根据|
|=|
|,求出P的纵坐标,然后求出三角形的面积即可.
| OP |
| OF |
解答:
解:双曲线
-y2=1(a>1)的一个焦点为F(
,0),
设P(asecθ,tanθ)θ∈(0,
),则
因为|
|=|
|,
所以,a2sec2θ+tan2θ=(
)2,解得tanθ=
,
所以△OPF的面积S=
•
•
=
.
故答案为:
.
| x2 |
| a2 |
| a2+1 |
设P(asecθ,tanθ)θ∈(0,
| π |
| 2 |
因为|
| OP |
| OF |
所以,a2sec2θ+tan2θ=(
| a2+1 |
|
所以△OPF的面积S=
| 1 |
| 2 |
| a2+1 |
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题是中档题,考查双曲线与向量的关系,求出P的纵坐标是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知全集U=R,集合A={x|x-1|<1},B={x|
≤0},则A∩(∁UB)=( )
| 1-x |
| x |
| A、(0,1) |
| B、[0,1) |
| C、(1,2) |
| D、(0,2) |
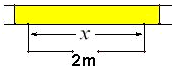 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米).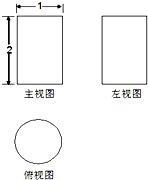 一个空间几何体的主视图和左视图都是矩形,俯视图是一个的圆,尺寸如图,那么这个几何体的侧面积为
一个空间几何体的主视图和左视图都是矩形,俯视图是一个的圆,尺寸如图,那么这个几何体的侧面积为