题目内容
数列{an}满足a1=1且对任意的m,n∈N*都有am+n=am+an+mn,则
+
+
+…+
=( )
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:取m=1,得an+1=an+(n+1),所以an=1+2+…+n=
,从而得到
=
=2(
-
),由此能求出
+
+
+…+
.
| n(n+1) |
| 2 |
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
解答:
解:∵数列{an}满足a1=1且对任意的m,n∈N*都有am+n=am+an+mn,
∴取m=1,得an+1=an+a1+n,即an+1=an+(n+1)
∴an=1+2+…+n=
,
∴
=
=2(
-
),
∴
+
+
+…+
=2(1-
+
-
+…+
-
)
=2×(1-
)=
.
故选:B.
∴取m=1,得an+1=an+a1+n,即an+1=an+(n+1)
∴an=1+2+…+n=
| n(n+1) |
| 2 |
∴
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=2×(1-
| 1 |
| 2014 |
| 4026 |
| 2014 |
故选:B.
点评:本题考查数列的前2013项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
一枚硬币连抛2次,只有一次出现正面的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
与
的夹角为120°,|
|=3,|
|=2,若
⊥
,
=λ
+
,则实数λ的值为( )
| AB |
| AC |
| AB |
| AC |
| AP |
| BC |
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
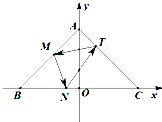 如图,点A,B,C的坐标分别为(0,2),(-2,0),(2,0),点M是边AB上异于A,B的一点,光线从点M出发,经BC,CA反射后又回到起点M.若光线NT交y轴于点(0,
如图,点A,B,C的坐标分别为(0,2),(-2,0),(2,0),点M是边AB上异于A,B的一点,光线从点M出发,经BC,CA反射后又回到起点M.若光线NT交y轴于点(0,| 2 |
| 3 |
A、(-
| ||||
B、(-
| ||||
| C、(-1,1) | ||||
D、(-
|
已知随机变量ξ-N(μ,2),且P(ξ≥1)=
,则实数μ的值为( )
| 1 |
| 2 |
| A、1 | ||
B、
| ||
| C、0 | ||
| D、2 |
已知x与y之间的几组数据如下表
则y与x的线性回归方程
=bx+a必过( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | -3 | -4 | -7 |
 |
| y |
| A、点(2,2) |
| B、点(1.5,4) |
| C、点(1.5,-3.75) |
| D、点(1.5,0) |
已知Sn是数列{an}的前n项和,Sn=an2+bn+c(a,b,c∈R),那么数列{an}( )
| A、不管a,b,c取何值是等差数列 |
| B、当a≠0时是等差数列 |
| C、当c=0时是等差数列 |
| D、不管a,b,c取何值都不是等差数列 |