题目内容
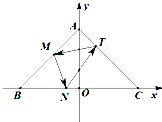 如图,点A,B,C的坐标分别为(0,2),(-2,0),(2,0),点M是边AB上异于A,B的一点,光线从点M出发,经BC,CA反射后又回到起点M.若光线NT交y轴于点(0,
如图,点A,B,C的坐标分别为(0,2),(-2,0),(2,0),点M是边AB上异于A,B的一点,光线从点M出发,经BC,CA反射后又回到起点M.若光线NT交y轴于点(0,| 2 |
| 3 |
A、(-
| ||||
B、(-
| ||||
| C、(-1,1) | ||||
D、(-
|
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:由题意易得AB、AC的方程,可设M的坐标,进而可表示M关于x轴的对称点M′和M关于AC的对称点M″的坐标,由三点共线可得.
解答:
解:∵A,B,C的坐标分别为(0,2),(-2,0),(2,0),
∴AB、AC的方程分别为:
+
=1,
+
=1,
故可设边AB上异于A,B的一点M为(a,a+2),
则M关于x轴的对称点M′(a,-a-2),
设M关于AC的对称点M″(m,n)
则
•(-1)=-1,且
+
=1,
解得m=-a,n=2-a,
由反射原理可知直线NT即为直线M′M″,
由M′、M″和(0,
)共线可得
=
,
解得a=-
,∴M(-
,
)
故选:B
∴AB、AC的方程分别为:
| x |
| -2 |
| y |
| 2 |
| x |
| 2 |
| y |
| 2 |
故可设边AB上异于A,B的一点M为(a,a+2),
则M关于x轴的对称点M′(a,-a-2),
设M关于AC的对称点M″(m,n)
则
| n-a-2 |
| m-a |
| m+a |
| 4 |
| a+2+n |
| 4 |
解得m=-a,n=2-a,
由反射原理可知直线NT即为直线M′M″,
由M′、M″和(0,
| 2 |
| 3 |
-a-2-
| ||
| a-0 |
2-a-
| ||
| -a-0 |
解得a=-
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
故选:B
点评:本题考查直线的对称性,利用好反射原理是解决问题的关键,属中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知cosα=-
,α∈(0,180°),则α的值是( )
| ||
| 2 |
| A、45° | B、125° |
| C、135° | D、145° |
已知平行四边形的3个顶点为A(a,b),B(-b,a),C(0,0),则它的第4个顶点D的坐标是( )
| A、(2a,b) |
| B、(a+b,b-a) |
| C、(a-b,a+b) |
| D、(a-b,b-a) |
数列{an}满足a1=1且对任意的m,n∈N*都有am+n=am+an+mn,则
+
+
+…+
=( )
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,如果输入a=2,那么输出的a值为( )


| A、4 |
| B、16 |
| C、256 |
| D、log316 |
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,则C的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| A、y=±2x | ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
已知i是虚数单位,(1+2i)z=i,则
=( )
. |
| z |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
交通局对上班、下班高峰时的车速情况作抽样调查,行驶时速(单位:km/h)的统计数据用茎叶图表示如图:
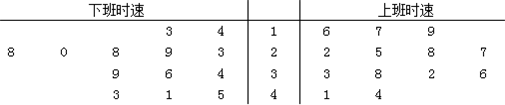
设上、下班时速的平均数分别为
上、
下,中位数分别为
上、
下,则( )

设上、下班时速的平均数分别为
. |
| x |
. |
| x |
. |
| m |
. |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|