题目内容
求函数z=1-
的值域.
|
考点:函数的值域
专题:函数的性质及应用
分析:根据二次根式
≥0,考查
的取值范围,即可得出函数的值域.
|
| 1-x2 |
| 4-x |
解答:
解:∵函数z=1-
,
∴
≥0,
即
≥0,
∴
≥0,
解得-1≤x≤1,或x>4;
∴当x∈{x|-1≤x≤1,或x>4}时,函数的值域是(-∞,1].
|
∴
|
即
| 1-x2 |
| 4-x |
∴
| (x+1)(x-1) |
| x-4 |
解得-1≤x≤1,或x>4;
∴当x∈{x|-1≤x≤1,或x>4}时,函数的值域是(-∞,1].
点评:本题考查了求函数值域的问题,解题的关键是利用二次根式的意义解答,是基础题.

练习册系列答案
相关题目
下列判断错误的是( )
| A、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||||
| B、命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | ||||
| C、函数y=2x-3+1的图象恒过定点A(3,2) | ||||
D、“sinα=
|
 已知椭圆C1:
已知椭圆C1: 已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足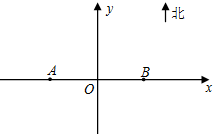 为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.
为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.