题目内容
14.已知函数满足一下两个条件:①任意x1,x2∈(0,+∞),且x1≠x2时,(x1-x2)[f(x1)-f(x2)]<0;②对定义域内任意x有f(x)+f(-x)=0,则符合条件的函数是( )| A. | f(x)=2x | B. | f(x)=1-|x| | C. | $f(x)=\frac{1}{x}-x$ | D. | f(x)=ln(x+1) |
分析 由①可知f(x)在(0,+∞)上是减函数,由②可知f(x)是奇函数.逐个分析各选项是否符合两条件即可.
解答 解:由①可知f(x)在(0,+∞)上是减函数,由②可知f(x)是奇函数.
对于A,f(x)=2x是增函数,不符合题意;
对于B,f(-x)+f(x)=1-|-x|+1-|x|=2-2|x|≠0,不符合题意,
对于D,f(x)的定义域为(-1,+∞),故f(x)不是奇函数,不符合题意;
故选C.
点评 本题考查了函数奇偶性与单调性的判断,属于中档题.

练习册系列答案
相关题目
9.若集合A={x|-1<x<2},B={x|-2<x<1},则集合A∪B=( )
| A. | {x|-1<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<2} | D. | {x|0<x<1} |
2.已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,圆C:x2+y2=6-a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1,椭圆M在点P处的切线斜率为k2,则$\frac{{k}_{1}}{{k}_{2}}$的取值范围为( )
| A. | (1,6) | B. | (1,5) | C. | (3,6) | D. | (3,5) |
3.一个几何体的三视图如图所示,则该几何体的表面积为( )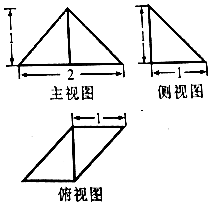

| A. | $\frac{3+\sqrt{3}+2\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}+\sqrt{2}}{2}$ | C. | $\frac{1+\sqrt{3}+2\sqrt{2}}{2}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |