题目内容
函数y=x2•cosx的导数为（ ）
| A、2xcosx+x2sinx |
| B、x2sinx-2xcosx |
| C、2xcosx-x2sinx |
| D、x2cosx-2xsinx |
考点：导数的运算
专题：导数的概念及应用
分析：根据的导数运算法则计算即可．
解答：
解：y′=2xcosx-x2•sinx．
故选：C．
故选：C．
点评：本题主要考查了导数的运算法则，属于基础题．
练习册系列答案
相关题目
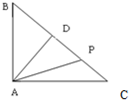如图，已知△ABC中，AB=3，AC=4，BC=5，AD⊥BC于D点，点P为BC边所在直线上的一个动点，则| AP |
| AD |
| A、最大值为9 | ||
B、为定值
| ||
| C、最小值为3 | ||
| D、与P的位置有关 |
函数y=f（x-4）的图象与函数y=f（2-x）的图象关于下列哪条直线对称（ ）
| A、x=3 | B、x=-1 |
| C、x=1 | D、x=-3 |
空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是（ ）
| A、垂直且相交 |
| B、相交但不一定垂直 |
| C、垂直但不相交 |
| D、不垂直也不相交 |
数列{an}中，a1=5，anan+1=2n，则
=（ ）
| a1 |
| a3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
函数f(x)=
-x的图象关于（ ）
| 1 |
| x |
| A、x轴对称 |
| B、y轴对称 |
| C、直线y=x对称 |
| D、坐标原点对称 |