题目内容
6.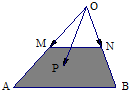 如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].
如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].
分析 根据P的位置分类讨论,利用向量的三角形法即可得解.
解答 解:P在MN上,可证:x+y=1,可得:4x+3y=4x+3-3x=x+3,x=0时,最小3,
P在AB上,可证:x+y=2,可得:4x+3y=4x+3(2-x)=x+6,x=2时,最大8,
则P落在阴影内,则有1<4x+3y<2.
故4x+3y的取值范围是[3,8],
故答案为:[3,8].
点评 本题考查向量的三角形法则,向量是数形结合的最好的工具,在解题时注意发挥向量的优点,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目
18.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)≤0.对任意正数a,b,若a<b,则必有( )
| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
 上为增函数的是( )
上为增函数的是( ) B.
B.
 D.
D.
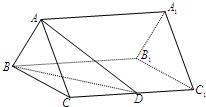 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°. 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点. 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.