题目内容
18.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)≤0.对任意正数a,b,若a<b,则必有( )| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
分析 由已知条件令F(x)=$\frac{f(x)}{x}$,判断出F′(x)≤0,据导函数的符号与函数单调性的关系判断出F(x)的单调性,利用单调性判断出F(a)与F(b)的关系,利用不等式的性质得到结论.
解答 解:∵f(x)是定义在(0,+∞)上的非负可导函数且满足xf′(x)≤f(x),
令F(x)=$\frac{f(x)}{x}$,则F′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵xf′(x)-f(x)≤0,
∴F′(x)≤0,
∴F(x)=$\frac{f(x)}{x}$在(0,+∞)上单调递减或常函数
∵对任意的正数a、b,a<b
∴$\frac{f(a)}{a}$≥$\frac{f(b)}{b}$,
∵任意的正数a、b,a<b,
∴af(b)≤bf(a)
故选:B.
点评 函数的导函数符号确定函数的单调性:当导函数大于0时,函数单调递增;导函数小于0时,函数单调递减.

练习册系列答案
相关题目
8.某产品40件,其中有次品数3件,现从中任取2件,则其中至少有一件次品的概率是( )
| A. | 0.1462 | B. | 0.1538 | C. | 0.9962 | D. | 0.8538 |
9.设离散型随机变量X的分布列为:
则p的值为( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
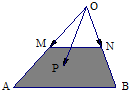 如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].
如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].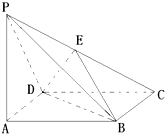 如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,
如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点, 已知正四棱锥P-ABCD,底面正方形的边长是2,高与斜高的夹角为30°,那么正四棱锥的侧面积为8.
已知正四棱锥P-ABCD,底面正方形的边长是2,高与斜高的夹角为30°,那么正四棱锥的侧面积为8.