题目内容
11．已知点A（2，0）B（0，-4）（1）写出△AOB的外接圆方程
（2）设直线l：3x-4y-1=0与△AOB的外接圆交于A，B两点，求|AB|
分析 （1）求出圆心与半径，即可写出△AOB的外接圆方程
（2）求出圆心到直线l：3x-4y-1=0的距离，利用勾股定理求|AB|．
解答 解：（1）由题意，圆心坐标为（1，-2），圆的半径为$\sqrt{5}$，
∴△AOB的外接圆方程为（x-1）2+（y+2）2=5；
（2）圆心到直线l：3x-4y-1=0的距离d=$\frac{|3+8-1|}{\sqrt{9+16}}$=2，
∴|AB|=2$\sqrt{5-4}$=2．
点评 本题考查圆的方程，考查直线与圆的位置关系，考查弦长公式，属于中档题．
练习册系列答案
相关题目
19．
如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：（1）SG⊥平面EFG；（2）SD⊥平面EFG；（3）GF⊥平面SEF；（4）EF⊥平面GSD；（5）GD⊥平面SEF．正确的是（ ）
如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：（1）SG⊥平面EFG；（2）SD⊥平面EFG；（3）GF⊥平面SEF；（4）EF⊥平面GSD；（5）GD⊥平面SEF．正确的是（ ）| A． | （1）和（3） | B． | （2）和（5） | C． | （1）和（4） | D． | （2）和（4） |
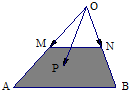如图所示，在△OAB中，M、N分别是OA、OB的中点，点P在梯形ABNM区域（含边界）上移动，且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$，则4x+3y的取值范围是[3，8]．
16．若正数a，b满足ab-（a+b）=1，则a+b的最小值是（ ）
| A． | 2+2$\sqrt{2}$ | B． | 2$\sqrt{2}$-2 | C． | $\sqrt{5}$+2 | D． | $\sqrt{5}$-2 |
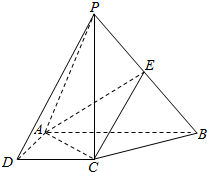如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，BC=$\sqrt{2}$，且PC⊥CD，BC⊥PA，E是PB的中点．