题目内容

17．设a1，a2，a3为正数，求证：$\frac{{a}_{1}{a}_{2}}{{a}_{3}}$+$\frac{{a}_{2}{a}_{3}}{{a}_{1}}$+$\frac{{a}_{3}{a}_{1}}{{a}_{2}}$≥a1+a2+a3．

分析 利用基本不等式，即可证明结论．

解答 证明：∵a1，a2，a3为正数，
∴$\frac{{a}_{1}{a}_{2}}{{a}_{3}}$+$\frac{{a}_{2}{a}_{3}}{{a}_{1}}$≥2a2，$\frac{{a}_{2}{a}_{3}}{{a}_{1}}$+$\frac{{a}_{3}{a}_{1}}{{a}_{2}}$≥2a3，$\frac{{a}_{1}{a}_{2}}{{a}_{3}}$+$\frac{{a}_{3}{a}_{1}}{{a}_{2}}$≥2a1，
三式相加，整理可得$\frac{{a}_{1}{a}_{2}}{{a}_{3}}$+$\frac{{a}_{2}{a}_{3}}{{a}_{1}}$+$\frac{{a}_{3}{a}_{1}}{{a}_{2}}$≥a1+a2+a3．

点评 本题考查不等式的证明，考查基本不等式的运用，正确运用基本不等式是关键．

练习册系列答案
相关题目
5．过原点且倾斜角为60°的直线被圆x2+y2-4x=0所截得的弦长为（　　）
A．$\sqrt{3}$B．2C．$\sqrt{6}$D．$2\sqrt{3}$
8．某产品40件，其中有次品数3件，现从中任取2件，则其中至少有一件次品的概率是（　　）
A．0.1462B．0.1538C．0.9962D．0.8538
5．若$f（n）=1+\frac{1}{{\sqrt{1}}}+\frac{1}{{\sqrt{2}}}+\frac{1}{{\sqrt{3}}}+…+\frac{1}{{\sqrt{n}}}$，（其中n＞2，且n∈N），$g（n）=2\sqrt{n}$，（其中n＞2，且n∈N），通过合情推理，试判断f（n）与g（n）的大小关系，并证明你的结论．
12．将5个小球放到3个盒子中，在下列条件下各有多少种投放方法：
（1）小球不同，盒子不同，盒子不空；
（2）小球不同，盒子不同，盒子可空；
（3）小球相同，盒子不同，盒子不空．
2．已知矩阵M=$[\begin{array}{l}{3}&{6}\\{2}&{2}\end{array}]$，则M的特征值为-1或6．
9．设离散型随机变量X的分布列为：
X1234
P$\frac{1}{6}$$\frac{1}{3}$$\frac{1}{6}$p
则p的值为（　　）
A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{6}$
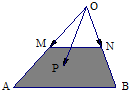6．如图所示，在△OAB中，M、N分别是OA、OB的中点，点P在梯形ABNM区域（含边界）上移动，且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$，则4x+3y的取值范围是[3，8]．
7．已知f（x）=$\frac{{{e^{ax}}}}{x}$，（e为自然对数的底数）．
（Ⅰ）若f（x）在（0，4]上是减函数，求实数a的取值范围；
（Ⅱ）当a=1时，求函数f（x）在[m，m+2]（m＞0）上的最小值；
（Ⅲ）求证：$\sum_{i=1}^n{\frac{1}{{i•{e^i}}}}＜\frac{7}{4e}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网