题目内容
已知二次函数y=f(x)满足f(0)=3,f(x+1)-f(x)=4x.
(1)求y=f(x)的解析式;
(2)求y=f(x)在[-1,1]上的最大值和最小值.
(1)求y=f(x)的解析式;
(2)求y=f(x)在[-1,1]上的最大值和最小值.
考点:抽象函数及其应用,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)设y=ax2+bx+c(a≠0),由f(0)=3得,c=3. 因为f(x+1)-f(x)=4x,所以2ax+a+b=4x,由此能够求出f(x).
(2)根据函数在[-1,1]上的单调性求出函数的最大值和最小值.
(2)根据函数在[-1,1]上的单调性求出函数的最大值和最小值.
解答:
解:设y=ax2+bx+c(a≠0)
由f(0)=3得,c=3
因为f(x+1)-f(x)=4x
所以a(x+1)2+b(x+1)-ax2-bx=4x,
即2ax+a+b=4x,
所以
解得a=2,b=-2,
所以y=2x2-2x+3,
(2)因为y=2x2-2x+3,对称轴x=
,
所以在[-1,
]单调递减,在(
,1]上单调递增,
所以当x=
时函数有最小值,最小值为
,
当x=-1时,函数有最大值,最大值为7,
由f(0)=3得,c=3
因为f(x+1)-f(x)=4x
所以a(x+1)2+b(x+1)-ax2-bx=4x,
即2ax+a+b=4x,
所以
|
解得a=2,b=-2,
所以y=2x2-2x+3,
(2)因为y=2x2-2x+3,对称轴x=
| 1 |
| 2 |
所以在[-1,
| 1 |
| 2 |
| 1 |
| 2 |
所以当x=
| 1 |
| 2 |
| 5 |
| 2 |
当x=-1时,函数有最大值,最大值为7,
点评:本题考查函数的解析式的求解及其常用方法,以及函数的单调性的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知底面边长为2cm,侧棱长为2
cm的正四棱柱各顶点都在同一球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、5
|
(
+
)8的展开式中x2的系数为( )
| x |
| 1 | ||
2
|
A、
| ||
B、
| ||
C、
| ||
| D、7 |
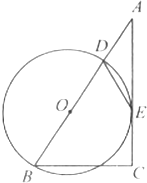 如图,在Rt△ABC中,∠A=30°,∠C=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E.若BC=6,则DE的长为
如图,在Rt△ABC中,∠A=30°,∠C=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E.若BC=6,则DE的长为 如图,某隧道设计为双向四车道,车道总宽20m,要求通过车辆限高5m,隧道全长2.5km,隧道两侧是与底面垂直的墙,高度为3m,隧道上部拱线近似地看成半个椭圆.
如图,某隧道设计为双向四车道,车道总宽20m,要求通过车辆限高5m,隧道全长2.5km,隧道两侧是与底面垂直的墙,高度为3m,隧道上部拱线近似地看成半个椭圆.