题目内容
点A(x0,y0)在双曲线
-
=1的右支上,若点A到右焦点的距离等于2x0,则x0= .
| x2 |
| 4 |
| y2 |
| 32 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题设条件先求出a,b,c,e,再由双曲线的第二定义,可得|AF|=e(x0-
),由此能求出x0的值.
| a2 |
| c |
解答:
解:双曲线
-
=1,可a=2,b=4
,c=6,
∴右焦点F(6,0),e=
=3,
把A(x0,y0)代入双曲线方程,得y02=8x02-32,
∴|AF|=
=
=2x0,
∴2x0=3(x0-
)=3(x0-
),
解得x0=2.
故答案为:2.
| x2 |
| 4 |
| y2 |
| 32 |
| 2 |
∴右焦点F(6,0),e=
| c |
| a |
把A(x0,y0)代入双曲线方程,得y02=8x02-32,
∴|AF|=
| (x0-6)2+y02 |
| (x0-6)2+8x02-32 |
∴2x0=3(x0-
| a2 |
| c |
| 2 |
| 3 |
解得x0=2.
故答案为:2.
点评:本题考查双曲线的方程和性质,以及第二定义的运用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
已知椭圆C:
+x2=1,过点P(
,
)的直线与椭圆C相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、4x+2y-3=0 |
| D、4x-2y-1=0 |
若x>0,y>0,则“x2+y2>1”是“x+y>1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
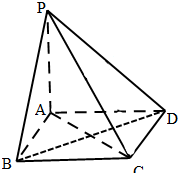 已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=
已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=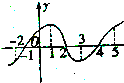 如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为
如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为 如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.
如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.