题目内容
{an}前n项和为Sn,a1=1,an=
+n-1.
(1)求证{an}为等差数列,并求其通项公式;
(2)若存在二次函数f(x)=ax2(a≠0)使数列{
}的前n项和Tn=
,求f(x).
| Sn |
| n |
(1)求证{an}为等差数列,并求其通项公式;
(2)若存在二次函数f(x)=ax2(a≠0)使数列{
| f(n) |
| anan+1 |
| 2n2+2n |
| 2n+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由an=
+n-1,可得Sn=nan-(n2-n),当n≥2时,Sn-1=(n-1)an-1-[(n-1)2-(n-1)],利用an=Sn-Sn-1,化为an-an-1=2,即可证明.
(2)
=
,当n=1时,
=
=
,解得a=4.可得f(x)=4x2.验证即可.
| Sn |
| n |
(2)
| f(n) |
| anan+1 |
| an2 |
| (2n-1)(2n+1) |
| f(1) |
| a1a2 |
| a |
| 3 |
| 2+2 |
| 3 |
解答:
(1)证明:∵an=
+n-1,∴Sn=nan-(n2-n),
当n≥2时,Sn-1=(n-1)an-1-[(n-1)2-(n-1)],
∴an=Sn-Sn-1=nan-(n2-n)-(n-1)an-1+[(n-1)2-(n-1)],化为an-an-1=2,
因此{an}为等差数列,
其通项公式an=1+2(n-1)=2n-1;
(2)解:
=
,
当n=1时,
=
=
,解得a=4.
∴f(x)=4x2.
∴
=
=
=1+
(
-
),
∴数列{
}的前n项和Tn=n+
[(1-
)+(
-
)+…+(
-
)]
=n+
(1-
)
=n+
=
.
满足已知条件,
∴f(x)=4x2.
| Sn |
| n |
当n≥2时,Sn-1=(n-1)an-1-[(n-1)2-(n-1)],
∴an=Sn-Sn-1=nan-(n2-n)-(n-1)an-1+[(n-1)2-(n-1)],化为an-an-1=2,
因此{an}为等差数列,
其通项公式an=1+2(n-1)=2n-1;
(2)解:
| f(n) |
| anan+1 |
| an2 |
| (2n-1)(2n+1) |
当n=1时,
| f(1) |
| a1a2 |
| a |
| 3 |
| 2+2 |
| 3 |
∴f(x)=4x2.
∴
| f(n) |
| anan+1 |
| 4n2 |
| (2n-1)(2n+1) |
| 4n2-1+1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴数列{
| f(n) |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=n+
| 1 |
| 2 |
| 1 |
| 2n+1 |
=n+
| n |
| 2n+1 |
=
| 2n2+2n |
| 2n+1 |
满足已知条件,
∴f(x)=4x2.
点评:本题考查了递推式的应用、“裂项求和”、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
复数
=( )
| 1+2i |
| 1-i |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
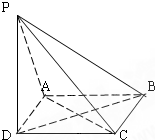

| A、过BD且与PC平行的平面交PA于M点,则M为PA的中点 |
| B、过AC且与PB垂直的平面交PB于N点,则N为PB的中点 |
| C、过AD且与PC垂直的平面交PC于H点,则H为PC的中点 |
| D、过P、B、C的平面与平面PAD的交线为直线l,则l∥AD |
已知椭圆C:
+x2=1,过点P(
,
)的直线与椭圆C相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、4x+2y-3=0 |
| D、4x-2y-1=0 |
已知3+sin2β+2t>(2
+
t)sin(β+
)+
对于β∈[0,
]恒成立,则t的取值范围是( )
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(
|
| π |
| 2 |
| A、t>4 | B、t>3 |
| C、t>2 | D、t≥-2 |
已知函数f(x)=sinωx+cosωx(ω>0),如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2015)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|