题目内容
(
+
)8的展开式中x2的系数为( )
| x |
| 1 | ||
2
|
A、
| ||
B、
| ||
C、
| ||
| D、7 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:由二项式定理,可得(
+
)8的展开式的通项,在其中令x的指数为0,解可得r的值,将r的值代入通项可得答案.
| x |
| 1 | ||
2
|
解答:
解:由二项式定理,可得(
+
)8的展开式的通项为Tr+1=C8r×(
)8-r×(
)r=(
)r×C8r×x4-r;
令4-r=2,解可得r=2;
则r=2时,T3=
×C82×x2=7x2;
即其展开式中x2的系数为7;
故选:D.
| x |
| 1 | ||
2
|
| x |
| 1 | ||
2
|
| 1 |
| 2 |
令4-r=2,解可得r=2;
则r=2时,T3=
| 1 |
| 4 |
即其展开式中x2的系数为7;
故选:D.
点评:本题考查二项式定理的运用,解题的关键在于准确运用二项式展开式的通项.

练习册系列答案
相关题目
已知a,b,c,d均为实数,下列命题中正确的是( )
| A、a>b⇒ac2>bc2 |
| B、a<b<0,c<d<0⇒ac<bd |
| C、a>b,ac<bc⇒c>0 |
| D、a>b,c>d⇒a+c>b+d |
若x>0,y>0,则“x2+y2>1”是“x+y>1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
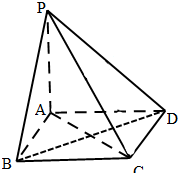 已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=
已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA= 如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.
如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.