题目内容
已知底面边长为2cm，侧棱长为2
cm的正四棱柱各顶点都在同一球面上，则该球的体积为（ ）
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、5
|
考点：球的体积和表面积,球内接多面体
专题：计算题,函数的性质及应用
分析：由长方体的对角线公式，算出正四棱柱体对角线的长，从而得到球直径长，得球半径R，最后根据球的体积公式，可算出此球的体积．
解答：
解：∵正四棱柱的底面边长为2cm，侧棱长为2
cm，
∴正四棱柱体对角线的长为
=2
又∵正四棱柱的顶点在同一球面上，
∴正四棱柱体对角线恰好是球的一条直径，得球半径R=
根据球的体积公式，得此球的体积为V=
πR3=
π．
故选：A．
| 3 |
∴正四棱柱体对角线的长为
| 4+4+12 |
| 5 |
又∵正四棱柱的顶点在同一球面上，
∴正四棱柱体对角线恰好是球的一条直径，得球半径R=
| 5 |
根据球的体积公式，得此球的体积为V=
| 4 |
| 3 |
20
| ||
| 3 |
故选：A．
点评：本题给出球内接正四棱柱的底面边长和侧棱长，求该球的体积，考查了正四棱柱的性质、长方体对角线公式和球的体积公式等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
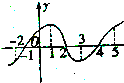如图所示的是函数y=f（x）的导函数y=f′（x）的图象，则[-2，5]上函数f（x）的递增区间为
如图，已知圆O：x2+y2=64分别与x轴、y轴的正半轴交于点A、B，直线l：y=kx-k+2分别于x轴、y轴的正半轴交于点N、M．