题目内容
画图:①利用单位圆寻找适合下列条件的0°到360°的角
1°sinα≥
2°tanα>
②求证:若0≤α1<α2≤
时,则sinα1<sinα2.
1°sinα≥
| 1 |
| 2 |
| ||
| 3 |
②求证:若0≤α1<α2≤
| π |
| 2 |
考点:单位圆与周期性
专题:数形结合法,三角函数的图像与性质
分析:画出图形,结合单位圆中表示正弦线、余弦线以及正切线的有向线段,即可得出正确的结论.
解答:
解:①,
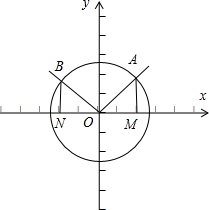
1°画出图形,如图所示,利用单位圆得:
满足sinα≥
在0°到360°的角是[30°,150°];
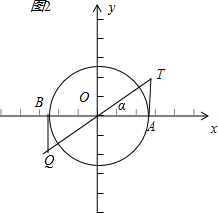
2°画出图形,如图2所示,利用单位圆得:
满足tanα>
在0°到360°的角是(30°,90°)∪(210°,270°);
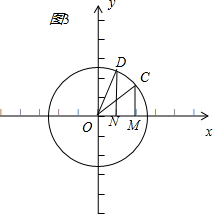
②证明:画出图形,如图3所示,
∠COM=α1,∠DON=α2,sinα1=MC,sinα2=DN,
∵0≤α1<α2≤
,
∴MC<ND,
即sinα1<sinα2.
1°画出图形,如图所示,利用单位圆得:
满足sinα≥
| 1 |
| 2 |
2°画出图形,如图2所示,利用单位圆得:
满足tanα>
| ||
| 3 |
②证明:画出图形,如图3所示,
∠COM=α1,∠DON=α2,sinα1=MC,sinα2=DN,
∵0≤α1<α2≤
| π |
| 2 |
∴MC<ND,
即sinα1<sinα2.



点评:本题考查了利用单位圆以及三角函数线求角的取值范围的问题,以及利用角判断三角函数值的大小的应用问题,是基础题目.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知集合A={x|x2-2x≤0,x∈R},集合B={x||x|≤1,x∈R},则A∩B为( )
| A、{x|0≤x≤2} |
| B、{x|1≤x≤2} |
| C、{x|-1≤x≤2} |
| D、{x|0≤x≤1} |
如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
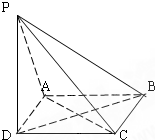

| A、过BD且与PC平行的平面交PA于M点,则M为PA的中点 |
| B、过AC且与PB垂直的平面交PB于N点,则N为PB的中点 |
| C、过AD且与PC垂直的平面交PC于H点,则H为PC的中点 |
| D、过P、B、C的平面与平面PAD的交线为直线l,则l∥AD |
已知椭圆C:
+x2=1,过点P(
,
)的直线与椭圆C相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、4x+2y-3=0 |
| D、4x-2y-1=0 |
已知a,b,c,d均为实数,下列命题中正确的是( )
| A、a>b⇒ac2>bc2 |
| B、a<b<0,c<d<0⇒ac<bd |
| C、a>b,ac<bc⇒c>0 |
| D、a>b,c>d⇒a+c>b+d |
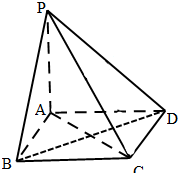 已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=
已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=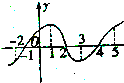 如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为
如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则[-2,5]上函数f(x)的递增区间为