题目内容
在正四面体P-ABC中,E,F分别是AB、PC中点,则异面直线BF与PE所成的角的余弦值为 .
考点:异面直线及其所成的角
专题:空间角
分析:连结CE,取CE中点G,连结FG,BG,由FG∥PE,得∠BFG是异面直线BF与PE所成的角,由此能求出异面直线BF与PE所成的角的余弦值.
解答:
解: 如图,连结CE,取CE中点G,连结FG,BG,
如图,连结CE,取CE中点G,连结FG,BG,
∵F是PC中点,G是CE中点,
∴FG∥PE,
∴∠BFG是异面直线BF与PE所成的角,
设正四面体P-ABC的棱长为1,
则PE=CE=BF=
=
,
∴FG=
PE=
,BG=
=
=
,
∴cos∠BFG=
=
.
∴异面直线BF与PE所成的角的余弦值为
.
故答案为:
.
 如图,连结CE,取CE中点G,连结FG,BG,
如图,连结CE,取CE中点G,连结FG,BG,∵F是PC中点,G是CE中点,
∴FG∥PE,
∴∠BFG是异面直线BF与PE所成的角,
设正四面体P-ABC的棱长为1,
则PE=CE=BF=
1-
|
| ||
| 2 |
∴FG=
| 1 |
| 2 |
| ||
| 4 |
| BE2+EG2 |
|
| ||
| 4 |
∴cos∠BFG=
(
| ||||||||||||
2×
|
| 2 |
| 3 |
∴异面直线BF与PE所成的角的余弦值为
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查直线与平面所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
一个样本容量为20的样本数据,它们组成一个等差数列{an},若a1=4,a20=42,则此样本的平均数和中位数分别是( )
| A、22,23 |
| B、23,22 |
| C、23,24 |
| D、23,23 |
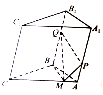 如图,在三棱柱ABC-A1B1C1的侧棱A1A和B1B上各有一个动点P,Q,且满足A1P=BQ,M是棱CA上的动点,则
如图,在三棱柱ABC-A1B1C1的侧棱A1A和B1B上各有一个动点P,Q,且满足A1P=BQ,M是棱CA上的动点,则