题目内容
一个样本容量为20的样本数据，它们组成一个等差数列{an}，若a1=4，a20=42，则此样本的平均数和中位数分别是（ ）
| A、22，23 |
| B、23，22 |
| C、23，24 |
| D、23，23 |
考点：等差数列的性质,众数、中位数、平均数
专题：计算题,等差数列与等比数列
分析：根据等差数列a1=4，a20=42，求出公差，再求数据的平均数和中位数．
解答：
解：设公差为d，
因为a1=4，a20=42，所以d=
=2
所以S20=20×4+
×2=460，
所以样本的平均数为
=23．
中位数为
=23．
故选：D．
因为a1=4，a20=42，所以d=
| 42-4 |
| 20-1 |
所以S20=20×4+
| 20×(20-1) |
| 2 |
所以样本的平均数为
| 460 |
| 20 |
中位数为
| a10+a11 |
| 2 |
故选：D．
点评：本题考查了等差数列的通项和前n项公式以及平均数，中位数的概念，属于基础题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）-g（x）在[a，b]上有两个不同的零点，则称f（x）与g（x）在[a，b]上是“关联函数”，区间[a，b]称为f（x）与g（x）的“关联区间”．若f（x）=
x3-x2-x与g（x）=2x+b的“关联区间”是[-3，0]，则b的取值范围是（ ）
| 1 |
| 3 |
| A、[-9，0] | ||
B、[0，
| ||
C、[0，
| ||
D、[-9，
|
在约束条件
下，则目标函数z=4x+2y的取值范围是（ ）
|
| A、[0，12] |
| B、[2，10] |
| C、[0，10] |
| D、[2，12] |
在平行四边形ABCD中，对角线AC与BD交于点O，
+
=λ
，则λ=（ ）
| AB |
| AD |
| AO |
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
若双曲线x2+
=1的离心率是2，则焦距为（ ）
| y2 |
| k |
| A、2 | ||
B、2
| ||
C、2
| ||
| D、4 |
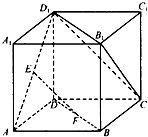如图，已知正方体ABCD-A1B1C1D1的棱长为1，E、F分别为AD1、BD的中点．