题目内容
若关于x的不等式mx2-2（m+1）x+m+3＞0的解集为R，则m的取值范围是 ．
考点：二次函数的性质
专题：不等式的解法及应用
分析：分别讨论m=0和m≠0，利用mx2-2（m+1）x+m+3＞0的解集为R，解出m的取值范围．
解答：
解：若m=0，则原不等式可化为-2x+3＞0，
此时不等式的解集不为R．
∴m=0不成立，即m≠0．
若m≠0，要使不等式mx2-2（m+1）x+m+3＞0的解集为R，
则m＞0时，且△=4（m+1）2-4m（m+3）＜0，
解得m＞1．
故m的取值范围是（1，+∞）
故答案为：（1，+∞）
此时不等式的解集不为R．
∴m=0不成立，即m≠0．
若m≠0，要使不等式mx2-2（m+1）x+m+3＞0的解集为R，
则m＞0时，且△=4（m+1）2-4m（m+3）＜0，
解得m＞1．
故m的取值范围是（1，+∞）
故答案为：（1，+∞）
点评：本题主要考查一元二次不等式的基本解法，恒成立问题，要注意分类讨论．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，椭圆C：
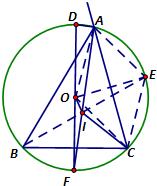如图，设O，I分别为△ABC的外心、内心，且∠B=60°，AB＞BC，∠A的外角平分线交⊙O于D，已知AD=18，则OI=．