题目内容
5.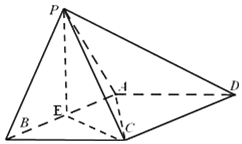 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E(1)证明:PE⊥平面ABCD;
(2)求三棱锥D-PBC的体积.
分析 (1)由题可知PE⊥AB,CE⊥AB.求解三角形可得PE=CE=$\sqrt{3}$.结合PC=$\sqrt{6}$,得PE2+EC2=PC2,可得PE⊥CE.再由线面垂直的判定可得PE⊥平面ABCD;
(2)由正弦定理求出S△BCD.然后利用等积法求得三棱锥D-PBC的体积.
解答 证明:(1)由题可知PE⊥AB,CE⊥AB.
∵AB=2,∴PE=CE=$\sqrt{3}$.
又∵PC=$\sqrt{6}$,∴PE2+EC2=PC2,
∴∠PEC=90°,即PE⊥CE.
又∵AB,CE?平面ABCD,
∴PE⊥平面ABCD;
解:(2)S△BCD=$\frac{1}{2}$×22×sin120°=$\sqrt{3}$,PE=$\sqrt{3}$.
由(1)知:PE⊥平面ABCD,
VP-BCD=$\frac{1}{3}$•S△BCD•PE=1.
∵VD-PBC=VP-BCD,
∴三棱锥D-PBC的体积为1.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.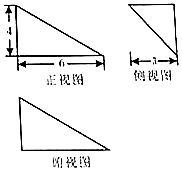 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )| A. | $\frac{\sqrt{61}}{6}$π | B. | $\frac{\sqrt{61}}{24}$π | C. | $\frac{61\sqrt{61}}{2}$π | D. | $\frac{61\sqrt{61}}{6}$π |
14.命题“存在x0∈R,2${\;}^{{x}_{0}}$≤0”的否定是( )
| A. | 不存在x0∈R,2${\;}^{{x}_{0}}$>0 | B. | 存在x0∈R,2${\;}^{{x}_{0}}$≥0 | ||
| C. | 对任意的x∈R,2x≤0 | D. | 对任意的x∈R,2x>0 |
15.某地区最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的线性回归方程$\hat y=\hat bx+\hat a$.
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)