题目内容
6.-400°的终边在哪个象限( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 先将-400°写成360°的整数倍加上一个0°到360°范围的角,再由此角的终边位置和象限角的定义进行判断.
解答 解:-400°=320°-2×360°
则-400°角与320°角的终边相同,即是第四象限角,
故选:D
点评 本题考查终边相同的角的定义,一般的方法是先将所给的角写成360°的整数倍加上一个0°到360°范围的角,则已知角与此角的终边相同.

练习册系列答案
相关题目
17.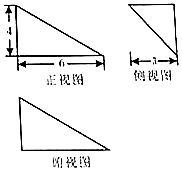 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )| A. | $\frac{\sqrt{61}}{6}$π | B. | $\frac{\sqrt{61}}{24}$π | C. | $\frac{61\sqrt{61}}{2}$π | D. | $\frac{61\sqrt{61}}{6}$π |
14.命题“存在x0∈R,2${\;}^{{x}_{0}}$≤0”的否定是( )
| A. | 不存在x0∈R,2${\;}^{{x}_{0}}$>0 | B. | 存在x0∈R,2${\;}^{{x}_{0}}$≥0 | ||
| C. | 对任意的x∈R,2x≤0 | D. | 对任意的x∈R,2x>0 |
15.某地区最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的线性回归方程$\hat y=\hat bx+\hat a$.
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
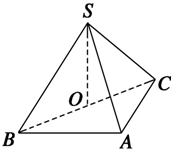 如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.