题目内容
1．已知函数g（x）=2x3+（2a+1）x+$\frac{1}{2}$，若曲线y=g（x）与x轴相切，则a的值为$-\frac{5}{4}$．分析 求函数的导数，利用导数的几何意义进行求解即可．
解答 解：函数g（x）=2x3+（2a+1）x+$\frac{1}{2}$，函数的导数f′（x）=6x2+2a+1，
∵x轴为函数g（x）=2x3+（2a+1）x+$\frac{1}{2}$的切线，
∴设过点为（m，0），
则2m3+（2a+1）m+$\frac{1}{2}$=0，①
又f′（m）=6m2+2a+1=0，②
由①②得m=$\frac{1}{2}$，a=-$\frac{5}{4}$，
故答案为：-$\frac{5}{4}$．
点评 本题主要考查导数的几何意义函数的极值的求法，设出切点坐标，求函数的导数，建立方程关系是解决本题的关键．
练习册系列答案
相关题目
6．两个相关变量满足如下关系：
根据表格已得回归方程：$\hat y$=9.4x+9.2，表中有一数据模糊不清，请推算该数据是（ ）
| x | 2 | 3 | 4 | 5 | 6 |
| y | 25 | ● | 50 | 56 | 64 |
| A． | 37.4 | B． | 39 | C． | 38.5 | D． | 40.5 |
16．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{{8\sqrt{2}}}{3}$ | D． | $\frac{{4\sqrt{2}}}{3}$ |
6．
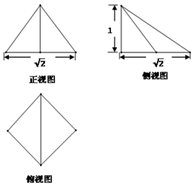如图是一个简单几何体的三视图，则该几何体的体积为（ ）
如图是一个简单几何体的三视图，则该几何体的体积为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 1 |
10．函数f（x）是定义在R上的奇函数，对任意两个正数x1，x2（x1＜x2）都有x2f（x1）＞x1f（x2），记a=$\frac{1}{2}$f（2），b=f（1），c=-$\frac{1}{3}$f（-3），则a，b，c之间的大小关系为（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞b＞a | D． | a＞c＞b |
11．2016年备受瞩目的二十国集团领导人第十一次峰会于9月4～5日在杭州举办，杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人，为测试培训效果，采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人，对其做G20峰会主题及相关服务职责进行测试，将其所得分数（分数都在60～100之间）制成频率分布直方图如下图所示，若得分在90分及其以上（含90分）者，则称其为“G20通”．
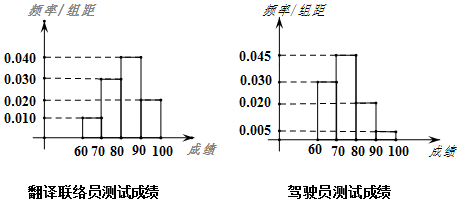
（Ⅰ）能否有90%的把握认为“G20通”与所从事工作（翻译联络员或驾驶员）有关？
（Ⅱ）从参加测试的成绩在80分以上（含80分）的驾驶员中随机抽取4人，4人中“G20通”的人数为随机变量X，求X的分布列与数学期望．
附参考公式与数据：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
（Ⅰ）能否有90%的把握认为“G20通”与所从事工作（翻译联络员或驾驶员）有关？
（Ⅱ）从参加测试的成绩在80分以上（含80分）的驾驶员中随机抽取4人，4人中“G20通”的人数为随机变量X，求X的分布列与数学期望．
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |