题目内容
9.函数y=acosx-$\frac{1}{a}$(a>0且a≠1)的图象可能是( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 讨论a的范围,根据指数函数和三角函数的性质得出y的范围和x=0时的函数值,从而得出函数图形的形状.
解答 解:若a>1,则当x=0时,y=a-$\frac{1}{a}$>0,
∵-1≤cosx≤1,∴y=acosx-$\frac{1}{a}$≥a-1-$\frac{1}{a}$=0,故A错误;
当0<a<1时,当x=0时,y=a-$\frac{1}{a}$<0,
∵-1≤cosx≤1,∴y=acosx-$\frac{1}{a}$≤a-1-$\frac{1}{a}$=0,故C正确,D错误,
综上可得,当x=0时,y≠0,故B错误;
故选:C.
点评 本题考查了函数图形的判定,利用三角函数和指数函数的性质得出y的符号是关键,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.若偶函数f(x)在(-∞,0]上单调递减,a=log2$\frac{1}{3}$,b=log4$\frac{1}{5}$,c=${2^{\frac{3}{2}}}$,则f(a),f(b),f(c)满足( )
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(a)<f(c) | C. | f(c)<f(a)<f(b) | D. | f(c)<f(b)<f(a) |
4.设函数y=f(x)在x=x0处取得极小值,则必有( )
| A. | f′(x0)=0 | B. | f″(x0)>0 | ||
| C. | f′(x0)=0且f″(x0)>0 | D. | f′(x0)=0或f′(x0)不存在 |
14.已知等比数列{an}的前n项和为Sn,若S3、S9、S6成等差数列,则下列说法错误的是( )
| A. | a3、a6、a9成等比数列 | B. | a3、a6、a9成等差数列 | ||
| C. | S2、S8、S5成等比数列 | D. | S2、S8、S5成等差数列 |
18.直线l1:ax+y-a+1=0,直线l1:4x+ay-2=0,则“a=±2”是“l1∥l2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
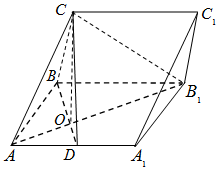 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.