题目内容
6.两个相关变量满足如下关系:| x | 2 | 3 | 4 | 5 | 6 |
| y | 25 | ● | 50 | 56 | 64 |
| A. | 37.4 | B. | 39 | C. | 38.5 | D. | 40.5 |
分析 根据回归方程过样本中心点,求得$\overline{y}$的值,从而求得看不清的数据a.
解答 解:计算$\overline{x}$=$\frac{1}{5}$×(2+3+4+5+6)=4,
根据回归方程$\hat y$=9.4x+9.2过样本中心点,
得$\overline{y}$=9.4×4+9.2=46.8;
设看不清的数据为a,则25+a+50+56+64=5$\overline{y}$=234,
解得a=39.
故选:C.
点评 本题考查了回归直线方程过样本中心点的应用问题,是基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
11.若偶函数f(x)在(-∞,0]上单调递减,a=log2$\frac{1}{3}$,b=log4$\frac{1}{5}$,c=${2^{\frac{3}{2}}}$,则f(a),f(b),f(c)满足( )
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(a)<f(c) | C. | f(c)<f(a)<f(b) | D. | f(c)<f(b)<f(a) |
4.设函数y=f(x)在x=x0处取得极小值,则必有( )
| A. | f′(x0)=0 | B. | f″(x0)>0 | ||
| C. | f′(x0)=0且f″(x0)>0 | D. | f′(x0)=0或f′(x0)不存在 |
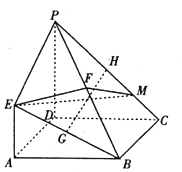 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.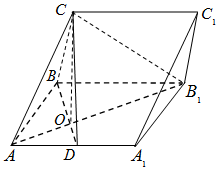 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.