题目内容
16．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{{8\sqrt{2}}}{3}$ | D． | $\frac{{4\sqrt{2}}}{3}$ |
分析 由三视图可知，该几何体是底面为边长为2的正方形，一条侧棱垂直底面的四棱锥，高为2，由体积公式计算体积即可．
解答 解：由三视图可知，该几何体是底面为边长为2的正方形，一条侧棱垂直底面的四棱锥，
高为2，故其体积V=$\frac{1}{3}×2×2×2=\frac{8}{3}$，
故选：A
点评 本题考查了空间几何体的三视图的应用问题，解题时应根据三视图，得出该几何体是什么图形，从而解答问题，是基础题．
练习册系列答案
相关题目
20．设复数z=$\frac{1-i}{1+i}$，其中i为虚数单位，则|z|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 3 |
4．设函数y=f（x）在x=x0处取得极小值，则必有（ ）
| A． | f′（x0）=0 | B． | f″（x0）＞0 | ||
| C． | f′（x0）=0且f″（x0）＞0 | D． | f′（x0）=0或f′（x0）不存在 |
8．若有一个线性回归方程为 $\stackrel{∧}{y}$=-2.5x+3，则变量x增加一个单位时（ ）
| A． | y平均减少2.5个单位 | B． | y平均减少0.5个单位 | ||
| C． | y平均增加2.5个单位 | D． | y平均增加0.5个单位 |
5．下列说法中正确的是（ ）
| A． | 一个命题的逆命题为真，则它的逆否命题一定为真 | |
| B． | 若“ac2＞bc2”，则a＞b | |
| C． | ?x0∈R，$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D． | “a2+b2=0，则a，b全为0”的逆否命题是“若a，b全不为0，则a2+b2≠0” |
6．
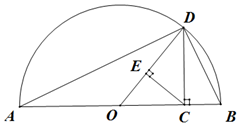若a＞0，b＞0，则称$\frac{2ab}{a+b}$为a，b的调和平均数．如图，点C为线段AB上的点，且AC=a，BC=b，点O为线段AB中点，以AB为直径做半圆，过点C作AB的垂线交半圆于D，连结OD，AD，BD．过点C作OD的垂线，垂足为E，则图中线段OD的长度是a，b的算术平均数，那么图中表示a，b的几何平均数与调和平均数的线段，以及由此得到的不等关系分别是（ ）
若a＞0，b＞0，则称$\frac{2ab}{a+b}$为a，b的调和平均数．如图，点C为线段AB上的点，且AC=a，BC=b，点O为线段AB中点，以AB为直径做半圆，过点C作AB的垂线交半圆于D，连结OD，AD，BD．过点C作OD的垂线，垂足为E，则图中线段OD的长度是a，b的算术平均数，那么图中表示a，b的几何平均数与调和平均数的线段，以及由此得到的不等关系分别是（ ）| A． | $CD，CE，\frac{2ab}{a+b}≥\sqrt{ab}$ | B． | $CD，DE，\frac{2ab}{a+b}≤\sqrt{ab}$ | C． | $CD，CE，\frac{2ab}{a+b}≥\sqrt{ab}$ | D． | $CD，CE，\frac{2ab}{a+b}≤\sqrt{ab}$ |