题目内容
8.在Rt△ABC中,∠ACB=90°,AC=1,BC=2,CD是∠ACB的角平分线(如图①).若沿直线CD将△ABC折成直二面角B-CD-A(如图②).则折叠后A,B两点间的距离为( )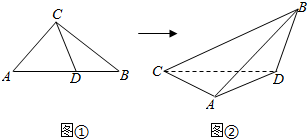
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 过A作CD的垂线AG,过B作CD的延长线的垂线BH,利用两条异面直线上两点间的距离公式求解.
解答 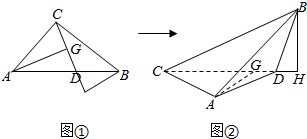 解:∵CD是∠ACB的角平分线,∴∠ACD=∠BCD=45°,
解:∵CD是∠ACB的角平分线,∴∠ACD=∠BCD=45°,
过A作CD的垂线AG,过B作CD的延长线的垂线BH,
∴AG=sin45°=$\frac{\sqrt{2}}{2}$,BH=2cos45°=$\sqrt{2}$,
CG=cos45°=$\frac{\sqrt{2}}{2}$,CH=2sin45°=$\sqrt{2}$,
则HG=CH-CG=$\sqrt{2}-\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
∴|AB|=$\sqrt{A{G}^{2}+B{H}^{2}+H{G}^{2}}$
=$\sqrt{\frac{1}{2}+2+\frac{1}{2}}$
=$\sqrt{3}$.
故选:B
点评 本题考查平面与平面之间的位置关系,考查了两条异面直线上两点间的距离,运用数学转化思想方法是解答该题的关键,是中档题.

练习册系列答案
相关题目
13.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为( )
| A. | 4 | B. | 3.5 | C. | 3 | D. | 2 |
15.已知函数f(2x-1)的定义域为[-1,4],则函数f(x)的定义域为( )
| A. | (-3,7] | B. | [-3,7] | C. | (0,$\frac{5}{2}$] | D. | [0,$\frac{5}{2}$) |
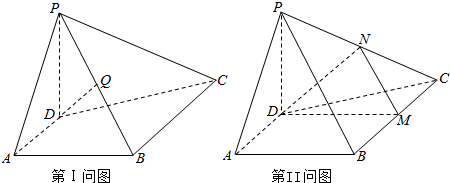
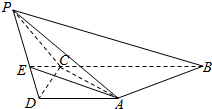 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.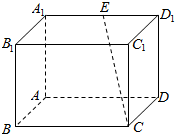 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.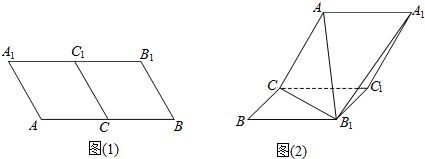
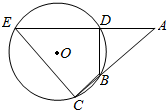 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A.