题目内容
3.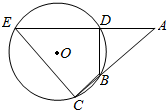 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A.(1)若BD⊥AE,AB=4,BC=2,AD=3,求CE的长;
(2)若$\frac{AB}{AC}$=$\frac{1}{2}$,$\frac{AD}{AE}$=$\frac{1}{3}$,求$\frac{BD}{EC}$的值.
分析 (1)首先根据题中圆的切线条件再依据割线定理求得一个线段AE的长,再根据勾股定理的线段的关系可求得CE的长度即可.
(2)由已知AC=2AB,AE=3AD,从而AD=$\frac{\sqrt{2}}{\sqrt{3}}AB$,由△ABD∽△AEC,能求出$\frac{BD}{EC}$的值.
解答 解:(1)∵⊙O的弦ED,CB的延长线交于点A,BD⊥AE,AB=4,BC=2,AD=3,
∴由割线定理得AB•AC=AD•AE,
∴AE=$\frac{AB•AC}{AD}$=$\frac{4×(4+2)}{3}$=8,
DE=AE-AD=8-3=5,
又BD⊥AE,∴BE为直径,∴∠C=90°,
在Rt△ACE中,由勾股定理得CE2=AE2-AC2=28,
∴CE=2$\sqrt{7}$.
(2)∵∠AEC=∠ABD,∠A=∠A,
∵$\frac{AB}{AC}$=$\frac{1}{2}$,$\frac{AD}{AE}$=$\frac{1}{3}$,∴AC=2AB,AE=3AD,
∵AD•AE=AB•AC,∴3AD2=2AB2,∴AD=$\frac{\sqrt{2}}{\sqrt{3}}AB$,
∴△ABD∽△AEC,∴$\frac{BD}{EC}$=$\frac{AB}{AE}$,
∴$\frac{BD}{EC}=\frac{AB}{3AD}=\frac{AB}{\frac{3\sqrt{2}}{\sqrt{3}}AB}$=$\frac{\sqrt{6}}{6}$.
点评 本题考查线段长的求法,考查两线段比值的求法,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
相关题目
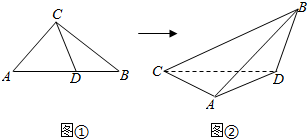
8.在Rt△ABC中,∠ACB=90°,AC=1,BC=2,CD是∠ACB的角平分线(如图①).若沿直线CD将△ABC折成直二面角B-CD-A(如图②).则折叠后A,B两点间的距离为( )

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
12.执行如图的框图,若输入k=30,则输出的n=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
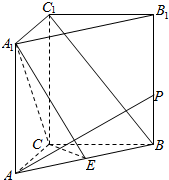 如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.
如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.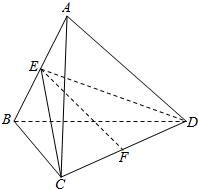 如图,正四面体ABCD的棱长为1.
如图,正四面体ABCD的棱长为1.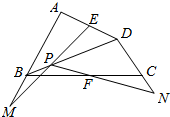 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.


