题目内容
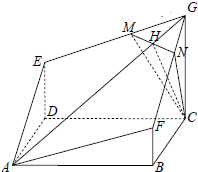
2.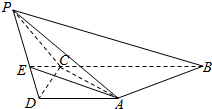 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.(Ⅰ)求证:平面PCD⊥平面PBC;
(Ⅱ)求证:PB∥平面AEC;
(Ⅲ)求四面体E-ABC的体积.
分析 (1)由CD⊥BC,CD⊥PB可证出CD⊥平面PBC,故平面PCD⊥平面PBC;
(2)连结BD交AC于O,连结OE,由△AOD∽△COB可得$\frac{OD}{OB}=\frac{AD}{BC}=\frac{1}{2}$,结合$\frac{DE}{PE}=\frac{1}{2}$可知OE∥PB,故而PB∥平面AEC;
(3)过P作PH⊥BC交BC延长线于H,所以PH=PC•sin60°=$\frac{\sqrt{3}}{2}$,从而求出E到底面ABC的距离h,从而求出棱锥的体积.
解答 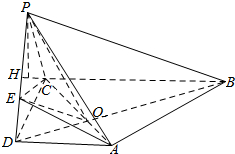 证明:(1)∵∠BCD=90°,∴CD⊥BC,
证明:(1)∵∠BCD=90°,∴CD⊥BC,
又∵CD⊥PB,PB?平面PBC,BC?平面PBC,BC∩PB=B,
∴CD⊥平面PBC,∵CD?平面PCD,
∴平面PCD⊥平面PBC.
(2)连结BD交AC于O,连结OE,
∵AD∥BC,∴△AOD∽△COB,∴$\frac{OD}{OB}=\frac{AD}{BC}=\frac{1}{2}$,
∵PE=2ED,∴$\frac{DE}{PE}=\frac{1}{2}$,∴$\frac{DE}{PE}=\frac{OD}{OB}$,
∴OE∥PB,∵OE?平面AEC,PB?平面AEC,
∴PB∥平面AEC.
(3)过P作PH⊥BC交BC延长线于H,
∵CD⊥平面PBC,CD?平面ABCD,
∴平面PBC⊥平面ABCD,∵平面PBC∩平面ABCD=BC,PH⊥BC,PH?平面PBC,
∴PH⊥平面ABCD.
∵∠PCB=120°,∴PH=PC•sin(π-120°)=$\frac{\sqrt{3}}{2}$.
∵PE=2ED,∴E到平面ABCD的距离h=$\frac{1}{3}$PH=$\frac{\sqrt{3}}{6}$.
∵S△ABC=$\frac{1}{2}$BC•CD=1,
∴V棱锥E-ABC=$\frac{1}{3}$S△ABC•h=$\frac{\sqrt{3}}{18}$.
点评 本题考查了线面垂直,线面平行的判定,棱锥的体积计算,属于中档题.

 阅读快车系列答案
阅读快车系列答案某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程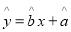 中的
中的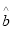 为
为 ,据此模型预报广告费用为6万元时销售额为 ( )
,据此模型预报广告费用为6万元时销售额为 ( )
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
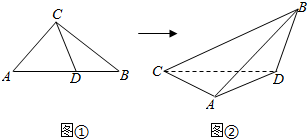
 如图是某直四棱柱被平面α所截得的部分,底面ABCD是矩形,侧棱GC、ED、FB都垂直于底面ABCD,GC=3,AB=2$\sqrt{2}$,BC=$\sqrt{5}$.
如图是某直四棱柱被平面α所截得的部分,底面ABCD是矩形,侧棱GC、ED、FB都垂直于底面ABCD,GC=3,AB=2$\sqrt{2}$,BC=$\sqrt{5}$. 如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.
如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.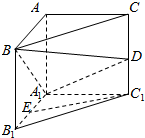 在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.