题目内容
已知:集合A={x|x≤-3,或x≥-1},B={x|2m<x<m-1,m∈R}.若A∪B=A,求实数m的取值范围.
考点:并集及其运算
专题:集合
分析:由A∪B=A说明集合B是集合A的子集,当集合B是空集时,符合题目条件,求出此时的a的范围,当B不是空集时,由两集合端点值之间的关系列不等式组求出m的范围,最后把两种情况求出的m的范围取并集即可.
解答:
解 因为A∪B=A,
所以B⊆A,
所以B可以是∅,此时2m>m-1,即m>-1
当B≠∅时,则m≤-1,
要使B⊆A,
所以m-1<-3或2m>-1,即m<-2或m>-
综上所述a的取值范围是m<-2或m>-
.
所以B⊆A,
所以B可以是∅,此时2m>m-1,即m>-1
当B≠∅时,则m≤-1,
要使B⊆A,
所以m-1<-3或2m>-1,即m<-2或m>-
| 1 |
| 2 |
综上所述a的取值范围是m<-2或m>-
| 1 |
| 2 |
点评:本题考查了并集及其运算,考查了集合之间的关系,考查了分类讨论的数学思想,解答此题的关键是由集合之间的关系得出它们的端点值之间的关系,是基础题也是易错题.

练习册系列答案
相关题目
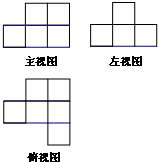 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )| A、6 | B、7 | C、8 | D、9 |
已知集合M={x|
≤1},N={x|y=lg(1-x)},则下列关系中正确的是( )
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
若sinα=
,cos(α+β)=-
,且α,β是锐角,则β等于( )
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=
为偶函数,则y=loga(x2-4x-5)的单调递增区间为( )
|
| A、(-∞,-1) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(5,+∞) |