题目内容
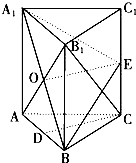 如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.
如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.(Ⅰ)求证:CD∥平面A1EB;
(Ⅱ)求证:平面AB1C⊥平面A1EB.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:
分析:(Ⅰ)说明三棱柱为正三棱柱,连结OD,证明CD∥EO,利用直线与平面平行的判定定理证明CD∥平面A1EB.
(Ⅱ)证明AB1⊥平面A1EB,通过平面与平面垂直的判定定理证明平面A1EB⊥平面AB1C.
(Ⅱ)证明AB1⊥平面A1EB,通过平面与平面垂直的判定定理证明平面A1EB⊥平面AB1C.
解答:
证明:(Ⅰ)∵棱柱的每个侧面为正方形,
∴
⇒AA1⊥底面ABC,
∴三棱柱为正三棱柱,
连结OD,
∵D为AB中点,O为对面线AB1,A1B交点,∴OD∥
BB1,
又E为CC1中点,∴EC∥
BB1,OD∥EC,
∴DCEO为平行四边形,CD∥EO,
又CD?平面A1EB,EO?平面A1EB,∴CD∥平面A1EB.
(Ⅱ)∵AB=AC=CB,∴CD⊥AB,
又直棱柱侧面ABB1A1⊥底面ABC,∴CD⊥平面ABB1A1,CD⊥AB1,
由(Ⅰ)CD∥EO,∴EO⊥AB1,
又正方形中,A1B⊥AB1,EO∩A1B=O,EO、A1B?平面A1EB,
∴AB1⊥平面A1EB,
又AB1?平面AB1C,∴平面A1EB⊥平面AB1C.
∴
|
∴三棱柱为正三棱柱,
连结OD,
∵D为AB中点,O为对面线AB1,A1B交点,∴OD∥
| 1 |
| 2 |
又E为CC1中点,∴EC∥
| 1 |
| 2 |
∴DCEO为平行四边形,CD∥EO,
又CD?平面A1EB,EO?平面A1EB,∴CD∥平面A1EB.
(Ⅱ)∵AB=AC=CB,∴CD⊥AB,
又直棱柱侧面ABB1A1⊥底面ABC,∴CD⊥平面ABB1A1,CD⊥AB1,
由(Ⅰ)CD∥EO,∴EO⊥AB1,
又正方形中,A1B⊥AB1,EO∩A1B=O,EO、A1B?平面A1EB,
∴AB1⊥平面A1EB,
又AB1?平面AB1C,∴平面A1EB⊥平面AB1C.
点评:本题考查直线与平面平行的判定定理以及平面与平面垂直的判定定理的应用,考查空间想象能力、逻辑推理能力.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
某几何体三视图如下图所示,则该几何体的表面积为( )


| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
已知集合M={x|
≤1},N={x|y=lg(1-x)},则下列关系中正确的是( )
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
若sinα=
,cos(α+β)=-
,且α,β是锐角,则β等于( )
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=
为偶函数,则y=loga(x2-4x-5)的单调递增区间为( )
|
| A、(-∞,-1) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(5,+∞) |
已知等比数列{an}的首项为
,公比为-
,其前n项和为Sn,则Sn的最大值为( )
| 3 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式x2-2x-3>0的解集是( )
| A、(-1,3) |
| B、(3,+∞) |
| C、(-∞,-1)∪(3,+∞) |
| D、(-∞,-1) |
已知集合A={-1,0,1},B={x|-1<x≤1},则A∩B=( )
| A、{0} | B、{-1,0} |
| C、{0,1} | D、{1} |