题目内容
4.把函数f(x)=sin(-3x+$\frac{π}{6}$)的周期扩大为原来的2倍,再将其图象向右平移$\frac{π}{3}$个单位长度,则所得图象的解析式为( )| A. | y=sin($\frac{π}{6}$-6x) | B. | y=cos6x | C. | y=sin($\frac{2π}{3}$-$\frac{3x}{2}$) | D. | y=sin(-$\frac{π}{6}$-$\frac{3}{2}$x) |
分析 先根据周期变为原来的2倍时ω的值变为原来的$\frac{1}{2}$倍得到y=sin(-$\frac{3}{2}$x+$\frac{π}{6}$),然后根据左加右减的平移原则可得答案.
解答 解:将函数f(x)=sin(-3x+$\frac{π}{6}$)的周期变为为原来的2倍得到y=sin(-$\frac{3}{2}$x+$\frac{π}{6}$),
向右平移$\frac{π}{3}$个单位长度,得到y=sin[-$\frac{3}{2}$(x-$\frac{π}{3}$)+$\frac{π}{6}$]=sin(-$\frac{3}{2}$x+$\frac{2π}{3}$).
故选:C.
点评 本题主要考查图象的平移和变换的知识.考查学生的基础知识的掌握程度,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
19.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B,若△ABF2是以∠ABF2为顶点的等腰直角三角形,则双曲线的离心率的平方为( )
| A. | 5+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3+2$\sqrt{2}$ |
13.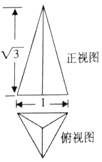 若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
 若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |