题目内容
14．已知函数f（x）=-（x+2）（x-m）（其中m＞-2），g（x）=2x-2．（1）命题p：f（x）≥0，命题q：g（x）＜0．，若p是q的充分非必要条件，求m的取值范围；
（2）设命题p：?x∈R，f（x）＜0或g（x）＜0：命题q：?x∈（-1，0）．f（x）•g（x）＜0，若p∧q是真命题，求m的取值范围．
分析 （1）由f（x）≥0，g（x）＜0求解不等式，再由p是q的充分非必要条件可得两不等式解集的关系，由集合端点值间的关系求得m的范围．
（2）由于p∧q是真命题，可得p与q都是真命题．由于当x＞1时，g（x）＞0，又p是真命题，可得f（x）＜0．由f（1）＜0，可得m＜1．当-1＜x＜0时，g（x）＜0．由于q是真命题，则?x∈（-1，0），使得f（x）＞0，利用f（-1）＞0，可得m的取值范围．
解答 解：（1）命题p：f（x）≥0，即-（x+2）（x-m）≥0，解得-2≤x≤m，
命题q：g（x）＜0，即2x-2＜0，解得x＜1，
∵p是q的充分非必要条件，
∴m＜1，
故m的取值范围为（-∞，1）；
（2）∵p∧q是真命题，∴p与q都是真命题．
当x＞1时，g（x）=2x-2＞0，又p是真命题，则f（x）＜0．
f（1）=-（1+2）（1-m）＜0，解得m＜1．
当-1＜x＜0时，g（x）=2x-2＜0．
∵q是真命题，则?x∈（-1，0），使得f（x）＞0，
∴f（-1）=-（-1+2）（-1-m）＞0，即m＞-1．
综上所述：-1＜m＜1．
点评 本题综合考查了二次函数和指数函数的单调性、简易逻辑的有关知识，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
4．把函数f（x）=sin（-3x+$\frac{π}{6}$）的周期扩大为原来的2倍，再将其图象向右平移$\frac{π}{3}$个单位长度，则所得图象的解析式为（ ）
| A． | y=sin（$\frac{π}{6}$-6x） | B． | y=cos6x | C． | y=sin（$\frac{2π}{3}$-$\frac{3x}{2}$） | D． | y=sin（-$\frac{π}{6}$-$\frac{3}{2}$x） |
2．
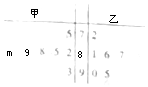甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{3}$ |