题目内容
9．a，b，c分别是△ABC内角A，B，C的对边，a+c=4，sinA（1+cosB）=（2-cosA）sinB，则△ABC面积的最大值为$\sqrt{3}$．分析 由正弦定理，余弦定理化简已知整理可得：2b=a+c，利用基本不等式可求ac的最大值，进而利用三角形面积公式即可计算得解．
解答 解：∵sinA（1+cosB）=（2-cosA）sinB，
∴由正弦定理可得：a（1+cosB）=b（2-cosA），
由余弦定理可得：a（1+$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$）=b（2-$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$），整理可得：2b=a+c，
∵a+c=4，可得：b=2，
∴16=（a+c）2≥4ac，解得：ac≤4，（当且仅当a=c=b=2等号成立，此时B=$\frac{π}{3}$），
∴S△ABC=$\frac{1}{2}acsinB$≤$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．
点评 本题主要考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角形中的综合应用，考查了转化思想，属于中档题．
练习册系列答案
相关题目
10．若a=60.3，b=log0.30.6，c=log6sin1，则a、b、c的大小关系为（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | b＞c＞a |
20．
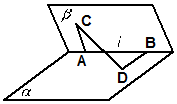如图，在二面角α-l-β的棱l上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，若二面角α-l-β的大小为$\frac{π}{3}$，AB=AC=2，BD=3，则CD=（ ）
如图，在二面角α-l-β的棱l上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，若二面角α-l-β的大小为$\frac{π}{3}$，AB=AC=2，BD=3，则CD=（ ）| A． | $\sqrt{11}$ | B． | $\sqrt{14}$ | C． | $2\sqrt{5}$ | D． | $\sqrt{23}$ |
17．执行如图所示的程序框图，输出S的值为（ ）
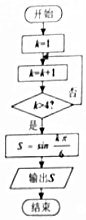
| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
4．把函数f（x）=sin（-3x+$\frac{π}{6}$）的周期扩大为原来的2倍，再将其图象向右平移$\frac{π}{3}$个单位长度，则所得图象的解析式为（ ）
| A． | y=sin（$\frac{π}{6}$-6x） | B． | y=cos6x | C． | y=sin（$\frac{2π}{3}$-$\frac{3x}{2}$） | D． | y=sin（-$\frac{π}{6}$-$\frac{3}{2}$x） |
14．已知输入的x=11，执行如图所示的程序框图，则输出的x的值为（ ）
| A． | 23 | B． | 47 | C． | 95 | D． | 191 |
1．已知全集U={1，2，3，4，5}，集合M={1，4}，N={1，3，5}，则（∁UM）∪（∁UN）=（ ）
| A． | {2，4} | B． | {2，3，5} | C． | {1，3，4，5} | D． | {2，3，4，5} |