题目内容
15.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),椭圆的离心率为$\frac{\sqrt{3}}{3}$.(1)求椭圆C的标准方程;
(2)过点F2的直线l与椭圆C相交于A,B两点,求△F1AB的面积的最大值.
分析 (1)由椭圆的焦点,离心率e,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)设直线l的方程为x=ty+1,代入2x2+3y2=6得得(2t2+3)y2+4ty-4=0,
由此利用韦达定理、弦长公式、换元法、函数单调性,结合已知条件能求出△F1PQ面积的最小值.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),
∴2c=2,c=1,又∵e=$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴$a=\sqrt{3}$,∵a2=b2+c2,∴$b=\sqrt{2}$
椭圆C的标准方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
(2)设直线l的方程为x=ty+1,代入2x2+3y2=6得得(2t2+3)y2+4ty-4=0,
∴y1+y2=$\frac{-4t}{2{t}^{2}+3}$,y1y2=$\frac{-4}{2{t}^{2}+3}$,
△F1AB的面积s=$\frac{1}{2}$2c•|y1-y2|=|y1-y2|=$\frac{4\sqrt{3}•\sqrt{{t}^{2}+1}}{2{t}^{2}+3}$,
令u=$\sqrt{1+{t}^{2}}$∈[1,+∞),则s=$\frac{4\sqrt{3}u}{2{u}^{2}+1}$=$\frac{4\sqrt{3}}{2u+\frac{1}{u}}$,
∵y=2u+$\frac{1}{u}$在[1,+∞)上是增函数,
∴当μ=1,即t=0时,△F1AB的面积的最小值是$\frac{4\sqrt{3}}{3}$.
点评 题考查椭圆方程的求法,考查三角形面积的最小值的求法,注意韦达定理、弦长公式、换元法、函数单调性的合理运用.属于中档题.

| A. | -2 | B. | 1 | C. | $\sqrt{3}$ | D. | -1 |
| A. | (-$\frac{5}{4}$,1) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{4}{5}$,1) | D. | (-1,$\frac{3}{4}$) |
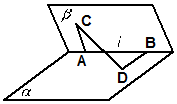 如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )| A. | $\sqrt{11}$ | B. | $\sqrt{14}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{23}$ |
| A. | y=sin($\frac{π}{6}$-6x) | B. | y=cos6x | C. | y=sin($\frac{2π}{3}$-$\frac{3x}{2}$) | D. | y=sin(-$\frac{π}{6}$-$\frac{3}{2}$x) |