题目内容
13．
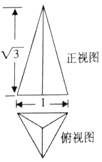若正三棱锥的正视图与俯视图如图所示，则它的侧视图的面积为（ ）| A． | $\sqrt{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{3}{4}$ |
分析 由三视图可知：作PO⊥底面ABC，点O为底面正△ABC的中心，连接CO延长与AB相交于点D，连接PD．CD⊥AB．则CD=$\frac{\sqrt{3}}{2}$，PO=$\sqrt{3}$．即可得出．
解答 解：由三视图可知：
作PO⊥底面ABC，点O为底面正△ABC的中心，连接CO延长与AB相交于点D，连接PD．CD⊥AB．
则CD=$\frac{\sqrt{3}}{2}$，PO=$\sqrt{3}$．
∴S侧视图=$\frac{1}{2}×\frac{\sqrt{3}}{2}×\sqrt{3}$=$\frac{3}{4}$．
故选：D
点评 本题考查了正三棱锥的三视图、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
4．把函数f（x）=sin（-3x+$\frac{π}{6}$）的周期扩大为原来的2倍，再将其图象向右平移$\frac{π}{3}$个单位长度，则所得图象的解析式为（ ）
| A． | y=sin（$\frac{π}{6}$-6x） | B． | y=cos6x | C． | y=sin（$\frac{2π}{3}$-$\frac{3x}{2}$） | D． | y=sin（-$\frac{π}{6}$-$\frac{3}{2}$x） |
1．已知全集U={1，2，3，4，5}，集合M={1，4}，N={1，3，5}，则（∁UM）∪（∁UN）=（ ）
| A． | {2，4} | B． | {2，3，5} | C． | {1，3，4，5} | D． | {2，3，4，5} |
8．命题“所有能被7整除的数都是奇数”的否定是（ ）
| A． | 所有不能被7整除的数都是奇数 | B． | 所有能被7整除的数都不是奇数 | ||
| C． | 存在一个不能被7整除的数是奇数 | D． | 存在一个能被7整除的数不是奇数 |
2．
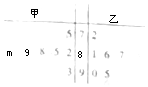甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示，两人各有一次成绩看不清楚，其中m，n∈Z，已知两位同学各自的7次成绩各不相同，但两人7次成绩的平均分相同，则两人7次成绩的中位数恰好也相同的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{3}$ |