题目内容
已知集合A={-2，-1，3，4}，B={x|x＞0}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：利用交集的性质求解．
解答：
解：∵集合A={-2，-1，3，4}，B={x|x＞0}，
∴A∩B={3，4}．
故答案为：{3，4}．
∴A∩B={3，4}．
故答案为：{3，4}．
点评：本题考查交集的求法，是基础题，解题时要注意交集性质的合理运用．
练习册系列答案
相关题目
函数y=x+
+5（x＞1）的最小值为（ ）
| 1 |
| x-1 |
| A、5 | B、6 | C、7 | D、8 |
三个数0.73.1，0.76，60.7的大小关系为（ ）
| A、0.73.1＜0.76＜60.7 |
| B、0.76＜0.73.1＜60.7 |
| C、0.76＜60.7＜0.73.1 |
| D、60.7＜0.76＜0.73.1 |
若复数z满足（1+i）z=i-2，则复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
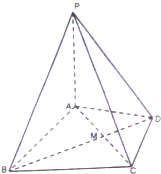如图，在四棱锥P-ABCD中，PA⊥面ABCD，△ABC是正三角形，AC△与BD的交点M恰好是AC的中点，又是PA=AB=2，∠CDA=120°．