题目内容
三棱锥A-BCD中，若AB⊥CD，AD⊥BC，则异面直线AC和BD所成的角为 ．
考点：异面直线及其所成的角
专题：空间角
分析：取特殊值法，由已知条件取三棱锥A-BCD为正四面体，由此能求出结果．
解答：
解：∵三棱锥A-BCD中，AB⊥CD，AD⊥BC，
∴三棱锥A-BCD可以是正四面体，
∴异面直线AC和BD所成的角为
．
故答案为：
．
∴三棱锥A-BCD可以是正四面体，
∴异面直线AC和BD所成的角为
| π |
| 2 |
故答案为：
| π |
| 2 |
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要注意特殊值法的合理运用．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若M={x|x＞1}，N={x|x≥a}，且N⊆M，则（ ）
| A、a≤1 | B、a≥1 |
| C、a＜1 | D、a＞1 |
如图，在正四棱锥P-ABCD中，底面为正方形，AB=2，VP-ABCD=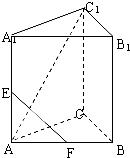
如图，在正三棱柱ABC-A1B1C1中，AC=2，AC1与底面成60°角，E、F分别为AA1、AB的中点．