题目内容
若复数z满足(1+i)z=i-2,则复数z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用复数的运算法则、几何意义即可得出.
解答:
解:由(1+i)z=i-2,
∴z=
=
=
所对应的点(-
,
)位于第二象限.
故选:B.
∴z=
| i-2 |
| 1+i |
| (i-2)(1-i) |
| (1+i)(1-i) |
| 3i-1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题考查了复数的运算法则、几何意义,属于基础题.

练习册系列答案
相关题目
函数f(x)的定义域为D,若满足:
①f(x)在D内是单调函数;
②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[-b,-a],那么y=f(x)叫做对称函数.
现有f(x)=
-k是对称函数,那么k的取值范围是( )
①f(x)在D内是单调函数;
②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[-b,-a],那么y=f(x)叫做对称函数.
现有f(x)=
| 2-x |
A、[2,
| ||||
B、(-∞,
| ||||
C、(2,
| ||||
D、(-∞,
|
设等差数列{an}的前n项的和Sn,若a5-a3=4,a4+a6=-10,则当Sn取最小时,n等于( )
| A、6 | B、7 | C、8 | D、9 |
已知α,β是两个不同的平面,l,m,n是不同的直线,则正确命题为( )
| A、若l⊥m,l⊥n,m?α,n?α,则l⊥α |
| B、若l∥m,m?α,则l∥α |
| C、若α⊥β,α∩β=l,m?α,m⊥l,则m⊥β |
| D、若α⊥β,l⊥α,则l∥β |
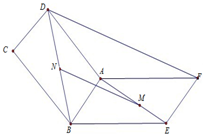 如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.
如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.