题目内容
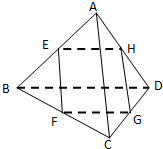 已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,(1)四边形EFGH是
(2)AC与BD所成角为60°,且AC=BD=1,则EG=
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由中位线易得EF∥AC且EF=
AC,GH∥AC且GH=
AC,可得平行四边形;
(2)由异面直线所成的角可得∠EFG=60°或120°,在△EFG中易得答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由异面直线所成的角可得∠EFG=60°或120°,在△EFG中易得答案.
解答:
解:(1)∵E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
∴EF为△ABC的AC边的中位线,故EF∥AC且EF=
AC,
同理GH为△ACD的AC边的中位线,故GH∥AC且GH=
AC,
∴EF平行且等于GH,∴四边形EFGH是平行四边形
(2)由(1)可得EF∥AC且EF=
AC=
,
同理FG∥BD且FG=
BD=
,
∵AC与BD所成角为60°,
∴∠EFG=60°或120°,
当∠EFG=60°时,EG=
;
当∠EFG=120°时,EG=
;
故答案为:平行四边;
或
∴EF为△ABC的AC边的中位线,故EF∥AC且EF=
| 1 |
| 2 |
同理GH为△ACD的AC边的中位线,故GH∥AC且GH=
| 1 |
| 2 |
∴EF平行且等于GH,∴四边形EFGH是平行四边形
(2)由(1)可得EF∥AC且EF=
| 1 |
| 2 |
| 1 |
| 2 |
同理FG∥BD且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC与BD所成角为60°,
∴∠EFG=60°或120°,
当∠EFG=60°时,EG=
| 1 |
| 2 |
当∠EFG=120°时,EG=
| ||
| 2 |
故答案为:平行四边;
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查空间中直线与直线的位置关系,涉及异面直线所成的角,属基础题.

练习册系列答案
相关题目
在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=3,则直线A1C与平面ABC1D1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一双曲线焦点的坐标,离心率分别为(±5,0)、
,则它的共轭双曲线的焦点坐标、离心率分别分别是( )
| 3 |
| 2 |
A、(0,±5),
| ||||||
B、(0,±5),
| ||||||
C、(0,±
| ||||||
D、(0,±
|
某几何体的立体图如图所示,该几何体的三视图不可能是( )
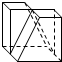

A、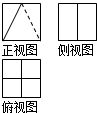 |
B、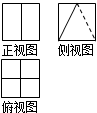 |
C、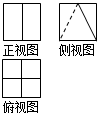 |
D、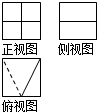 |